题目内容
下列不等式成立的是( )
A. | B. |
C. | D. |
A
解析试题分析:因为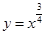 在第一象限单调递增,所以
在第一象限单调递增,所以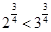 ;又因为
;又因为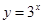 单调递增,所以
单调递增,所以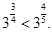 所以选项A正确.利用对数函数的单调性及中间值1,可以判断出选项B,C,D不正确.
所以选项A正确.利用对数函数的单调性及中间值1,可以判断出选项B,C,D不正确.
考点:本小题主要考查利用指数函数、对数函数、幂函数的单调性比较数的大小,考查学生准确利用函数性质解决实际问题的能力.
点评:准确掌握三种函数的单调性并灵活应用是解题的关键,有时还要利用0或1作中间值.

练习册系列答案
相关题目
2log510+log50.25=
| A.0 | B.1 | C.2 | D.4 |
已知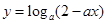 在
在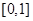 上是
上是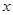 的减函数,则
的减函数,则 的取值范围是( )
的取值范围是( )
A.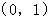 | B.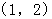 | C.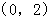 | D.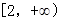 |
已知幂函数 过点
过点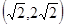 ,则函数
,则函数 的表达式为( )
的表达式为( )
A. | B. | C. | D.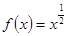 |
下列各式中成立的是( )
A. | B. |
C. | D. |
 ,
, ,那么( )
,那么( )
A. | B. | C. | D. |
已知函数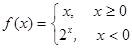 ,则
,则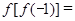 ( )
( )
A. | B.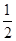 | C.1 | D.2 |
已知 那么
那么
A. | B. | C. | D. |
设函数 ,则
,则 ( )
( )
A. | B. | C. | D.3 |