题目内容
已知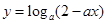 在
在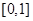 上是
上是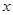 的减函数,则
的减函数,则 的取值范围是( )
的取值范围是( )
A.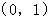 | B.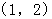 | C.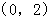 | D.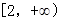 |
B
解析试题分析:原函数是由简单函数t=2-ax和y=logat共同复合而成.
∵a>0,∴t=2-ax为定义域上减函数,
而由复合函数法则和题意得到,
y=logat在定义域上为增函数,∴a>1
又函数t=2-ax>0在(0,1)上恒成立,则2-a<0即可.
∴a<2.综上,1<a<2,
故答案为B
考点:本题主要考查了复合函数单调性的运用。
点评:解决该试题的关键是解决对数函数问题时,注意真数位置的范围.本题中如若不注意这一点,会导致答案错误的为(1,+∞).这也是考生的易错点.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
已知 ,
, ,则
,则 ( )
( )
| A.3 | B.8 | C.4 | D. |
已知函数 ,则
,则 ( )
( )
| A.4 | B. | C.-4 | D.- |
若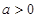 ,且
,且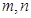 为整数,则下列各式中正确的是
为整数,则下列各式中正确的是
A. | B. |
C. | D. |
已知函数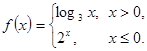 则
则 的值为( )
的值为( )
A.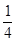 | B.4 | C.2 | D.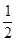 |
函数f (x)=(m2-m-1)x 是幂函数,且在x∈(0,+∞)上是减函数,那么实数
是幂函数,且在x∈(0,+∞)上是减函数,那么实数
m的值为
A. | B.-2 | C. | D.2 |
三个数 ,
, 之间的大小关系是( )
之间的大小关系是( )
A. ﹤ ﹤ ﹤ ﹤ | B. ﹤ ﹤ ﹤ ﹤  | C. ﹤ ﹤ ﹤ ﹤ | D. ﹤ ﹤ ﹤ ﹤ |
下列不等式成立的是( )
A. | B. |
C. | D. |
设函数 ,若
,若 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |