题目内容
定义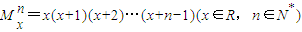 ,如
,如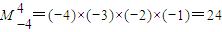 .对于函数
.对于函数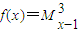 ,则函数f(x)的解析式是: ,且f(x)的单调递减区间是 (写成开区间或闭区间都给全分).
,则函数f(x)的解析式是: ,且f(x)的单调递减区间是 (写成开区间或闭区间都给全分).
【答案】分析:求导函数,利用导数小于0,解不等式,即可得到结论.
解答:解:∵f(x)=(x-1)•x•(x+1)=x3-x,
又由f′(x)=3x2-1<0,得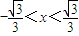
即f(x)的单调减区间为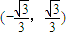 .
.
故答案为:f(x)=x3-x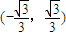
点评:本题考查导数知识的运用,考查函数的单调性,解题的关键是求导函数,利用导数小于0,确定函数的单调减区间.
解答:解:∵f(x)=(x-1)•x•(x+1)=x3-x,
又由f′(x)=3x2-1<0,得
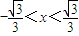
即f(x)的单调减区间为
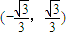 .
.故答案为:f(x)=x3-x
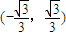
点评:本题考查导数知识的运用,考查函数的单调性,解题的关键是求导函数,利用导数小于0,确定函数的单调减区间.

练习册系列答案
相关题目
 ,如
,如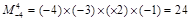 .对于函数
.对于函数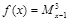 ,给出下列四个命题:①f (x)的最大值为
,给出下列四个命题:①f (x)的最大值为 ;②f (x)为奇函数;③f(x)的图象不具备对称性;④f (x)在
;②f (x)为奇函数;③f(x)的图象不具备对称性;④f (x)在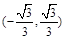 上是减函数,真命题是 ▲
(填命题序号).
上是减函数,真命题是 ▲
(填命题序号).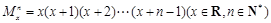 ,如
,如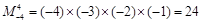 .
.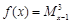 ,则函数
,则函数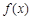 的解析式是:
的解析式是: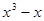 ,且
,且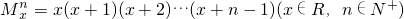 ,如
,如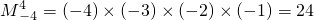 .对于函数
.对于函数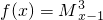 ,则函数f(x)的解析式是:________,且f(x)的单调递减区间是________(写成开区间或闭区间都给全分).
,则函数f(x)的解析式是:________,且f(x)的单调递减区间是________(写成开区间或闭区间都给全分).