题目内容
11.已知函数f(x)=$\frac{1+ln(x-1)}{x-1}$(x∈[2,+∞)).(1)若不等f(x)≥$\frac{m}{x}$对任意x≥2恒成立,求m的范围;
(2)证明:对任意n∈Z,均有n-ln(n+1)<2($\frac{1}{2}+\frac{2}{3}+$…+$\frac{n}{n+1}$).
分析 (1)把不等f(x)≥$\frac{m}{x}$对任意x≥2恒成立转换为f(x)x≥m恒成立,利用导数求出函数的最小值,只需最小值≥m
(2)想到(1)的结论,当m=2时,不等式ln(x-1)≥1-$\frac{2}{x}$利用放缩法得出ln(x-1)≥1-$\frac{2}{x-1}$,进而关联到本题的特点,令$\frac{k+1}{k}$=x-1则ln$\frac{k+1}{k}$>1-$\frac{2k}{k+1}$.从而分别令k=1,2,3…,得出结论.
解答 解:(1)f(x)≥$\frac{m}{x}$对任意x≥2恒成立
∴$\frac{1+ln(x-1)}{x-1}$•x≥m恒成立 (x∈[2,+∞))
令h(x)=$\frac{1+ln(x-1)}{x-1}$•x
∴h′(x)=$\frac{(x-1)-ln(x-1)}{(x-1)^{2}}$
令g(x)=(x-1)-ln(x-1)
∴g′(x)=$\frac{x-2}{x-1}$>0
∴g(x)在x∈[2,+∞)上递增
∴g(x)≥g(2)=1>0
∴h′(x)=$\frac{(x-1)-ln(x-1)}{(x-1)^{2}}$>0
∴h(x)在x∈[2,+∞)上递增
∴h(x)min=h(2)=2
∴m≤2
(2)由(1)得:x≥2时,f(x)≥$\frac{2}{x}$
即$\frac{1+ln(x+1)}{x-1}$≥$\frac{2}{x}$
整理得ln(x-1)≥1-$\frac{2}{x}$>1-$\frac{2}{x-1}$
令$\frac{k+1}{k}$=x-1则
ln$\frac{k+1}{k}$>1-$\frac{2k}{k+1}$
k=1时,1-2×$\frac{1}{2}$<ln 2
k=2时,1-2×$\frac{2}{3}$<ln $\frac{3}{2}$
…,
k=n时,1-2 $\frac{n}{n+1}$<ln $\frac{n+1}{n}$
将以上不等式两端分别相加得:
n-2($\frac{1}{2}$+$\frac{2}{3}$+…+$\frac{n}{n+1}$)<ln(2×$\frac{3}{2}$×…×$\frac{n+1}{n}$)=ln(n+1)
整理得n-ln(n+1)<2($\frac{1}{2}+\frac{2}{3}+$…+$\frac{n}{n+1}$).
点评 考察了恒成立问题和利用导数求函数最值,利用题中结论分析问题,解决问题.技能要求比较高.

 ,则
,则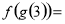 ( )
( )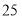 B.
B. 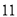 C.
C.  D.
D.