题目内容
若三条射线OA、OB、OC两两成角60°,则直线OA与平面OBC所成的角为分析:由题意,从同一点O出发的三条射线两两成60°,所以此三棱锥为正四面体,设棱长为a,因为三棱锥从同一点O出发的三条射线两两成60°,所有侧棱长都应为a,且OA在底面OBC内的射影应在底面OBC中∠BOC的角平分线上,点A在底面内的投影点也应为底面这一正三角形的中心,然后在直角三角形中即可求解.
解答: 解:由题意作出如下图形:
解:由题意作出如下图形:
∵三条射线OA、OB、OC两两成角60°,
∴OA在底面的射影为∠BOC的角平分线即为OH,
又∵两两成60°,
∴不妨假设OA=OB=OC=a,则此三棱锥的所有棱长都为a,
∴H也应为底面三角形的中心即为点H,
∴OH=
a,在直角三角形OAH中以求得cos∠AOH=
,
有反三角函数知识可知OA与底平面的线面角既是∠AOH=arccos
,
故答案为:arccos
.
 解:由题意作出如下图形:
解:由题意作出如下图形:∵三条射线OA、OB、OC两两成角60°,
∴OA在底面的射影为∠BOC的角平分线即为OH,
又∵两两成60°,
∴不妨假设OA=OB=OC=a,则此三棱锥的所有棱长都为a,
∴H也应为底面三角形的中心即为点H,
∴OH=
| ||
| 3 |
| ||
| 3 |
有反三角函数知识可知OA与底平面的线面角既是∠AOH=arccos
| ||
| 3 |
故答案为:arccos
| ||
| 3 |
点评:此题重点考查了直线与平面所成的线面角的概念及求解,还考查了做题时的特殊化解决问题的技巧,还考查了直角三角形中解角的技巧及用反三角函数求解角的大小这一知识.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
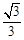 B.
B. 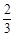 C.
C. 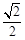 D.
D.