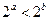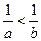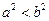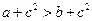题目内容
设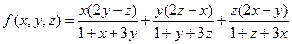 ,其中
,其中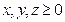 ,且
,且
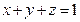 .求
.求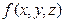 的最大值和最小值.
的最大值和最小值.
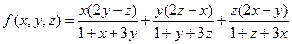 ,其中
,其中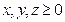 ,且
,且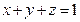 .求
.求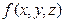 的最大值和最小值.
的最大值和最小值.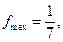
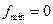
:先证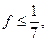 当且仅当
当且仅当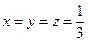 时等号成立.
时等号成立.
因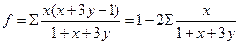 …
… 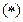
由哥西不等式: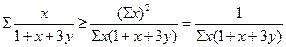 ,因为
,因为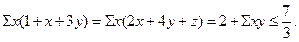
从而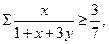
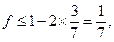
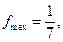 当且仅当
当且仅当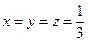 时等号成立.
时等号成立.
再证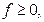 当
当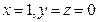 时等号成立.
时等号成立.
事实上,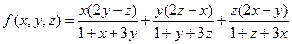 =
=
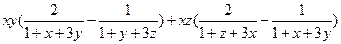
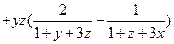
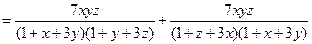
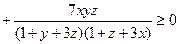
故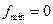 ,当
,当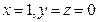 时等号成立.
时等号成立.
另证:设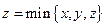 ,若
,若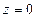 ,则
,则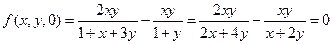 ;
;
下设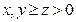 ,由
,由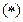 式,要证
式,要证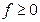 ,只要证,
,只要证,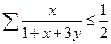 …①
…①
注意到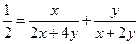 ,于是①等价于
,于是①等价于
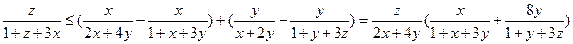 即
即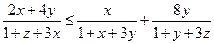 …②
…②
而由柯西不等式,可得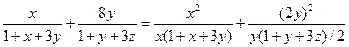
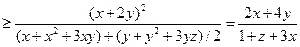
即②成立,从而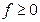 ,故
,故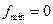 ,当
,当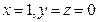 时等号成立.
时等号成立.
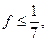 当且仅当
当且仅当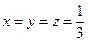 时等号成立.
时等号成立.因
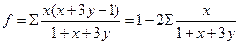 …
… 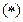
由哥西不等式:
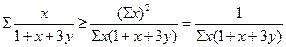 ,因为
,因为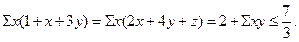
从而
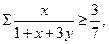
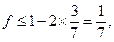
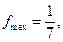 当且仅当
当且仅当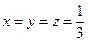 时等号成立.
时等号成立.再证
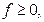 当
当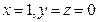 时等号成立.
时等号成立.事实上,
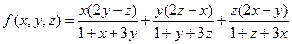 =
=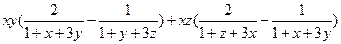
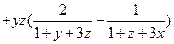
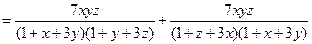
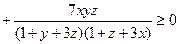
故
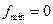 ,当
,当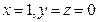 时等号成立.
时等号成立.另证:设
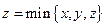 ,若
,若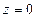 ,则
,则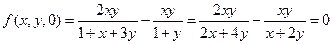 ;
;下设
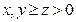 ,由
,由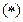 式,要证
式,要证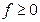 ,只要证,
,只要证,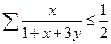 …①
…①注意到
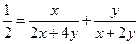 ,于是①等价于
,于是①等价于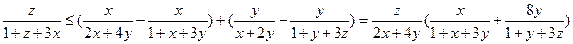 即
即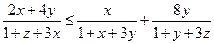 …②
…②而由柯西不等式,可得
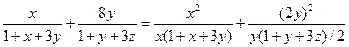
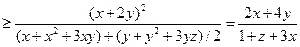
即②成立,从而
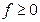 ,故
,故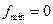 ,当
,当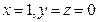 时等号成立.
时等号成立.
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
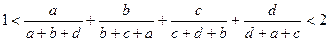
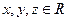 ,且
,且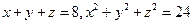
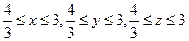
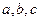 为互不相等的正数,
为互不相等的正数,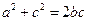 ,则下列关系中可能成立的是( )
,则下列关系中可能成立的是( )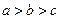
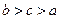
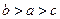
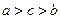
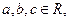 且
且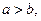 则下列结论正确的是
则下列结论正确的是