题目内容
已知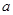 为实数,数列
为实数,数列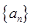 满足
满足 ,当
,当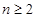 时,
时,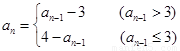 ,
,
(Ⅰ)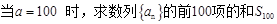 ;(5分)
;(5分)
(Ⅱ)证明:对于数列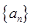 ,一定存在
,一定存在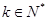 ,使
,使 ;(5分)
;(5分)
(Ⅲ)令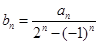 ,当
,当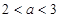 时,求证:
时,求证: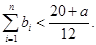 (6分)
(6分)
【答案】
(Ⅰ)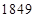 ;(Ⅱ)详见解析;(Ⅲ)详见解析
;(Ⅱ)详见解析;(Ⅲ)详见解析
【解析】
试题分析:(Ⅰ)根据题意可得当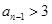 时,
时,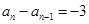 成等差数列,当
成等差数列,当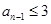 时,
时,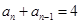 ,可见由
,可见由 得出前
得出前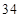 项成等差数列,
项成等差数列,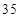 项以后奇数项为
项以后奇数项为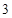 ,偶数项为
,偶数项为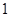 ,这样结合等差数列的前
,这样结合等差数列的前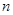 项公式就可求出
项公式就可求出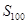 ;(Ⅱ)以
;(Ⅱ)以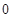 和
和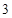 为界对
为界对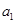 进行分类讨论,当
进行分类讨论,当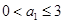 时,显然成立;当
时,显然成立;当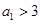 时,由题中所给数列的递推关系
时,由题中所给数列的递推关系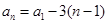 ,不难得到
,不难得到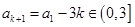 ;当
;当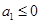 时,得
时,得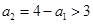 ,可转化为当
,可转化为当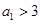 时的情况,命题即可得证; (Ⅲ)由
时的情况,命题即可得证; (Ⅲ)由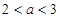 可得
可得 ,根据题中递推关系可得出
,根据题中递推关系可得出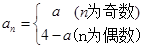 ,进而可得出
,进而可得出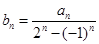 =
=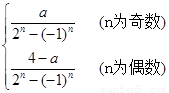 ,又
,又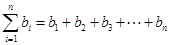 ,由于
,由于 要对
要对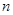 分奇偶性,故可将相邻两整数
分奇偶性,故可将相邻两整数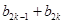 当作一个整体,要证不等式可进行适当放缩
当作一个整体,要证不等式可进行适当放缩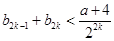 ,要对
,要对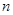 分奇偶性,并结合数列求和的知识分别进行证明即可.
分奇偶性,并结合数列求和的知识分别进行证明即可.
试题解析:(Ⅰ)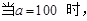 由题意知数列
由题意知数列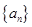 的前34项成首项为100,公差为-3的等差数列,从第35项开始,奇数项均为3,偶数项均为1,从而
的前34项成首项为100,公差为-3的等差数列,从第35项开始,奇数项均为3,偶数项均为1,从而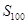 =
=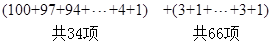 (3分)
(3分)
=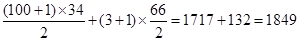 .
(5分)
.
(5分)
(Ⅱ)证明:①若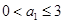 ,则题意成立
(6分)
,则题意成立
(6分)
②若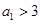 ,此时数列
,此时数列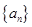 的前若干项满足
的前若干项满足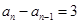 ,即
,即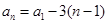 .
.
设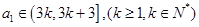 ,则当
,则当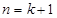 时,
时,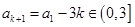 .
.
从而此时命题成立 (8分)
③若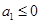 ,由题意得
,由题意得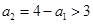 ,则由②的结论知此时命题也成立.
,则由②的结论知此时命题也成立.
综上所述,原命题成立 (10分)
(Ⅲ)当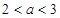 时,因为
时,因为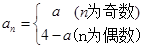 ,
,
所以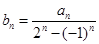 =
=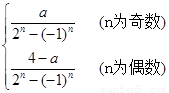 (11分)
(11分)
因为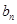 >0,所以只要证明当
>0,所以只要证明当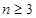 时不等式成立即可.
时不等式成立即可.
而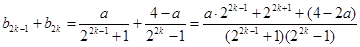
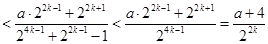 (13分)
(13分)
①当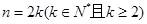 时,
时,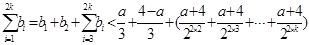
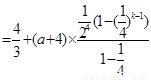
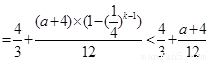
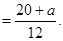 (15分)
(15分)
②当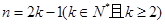 时,由于
时,由于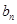 >0,所以
>0,所以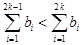 <
<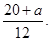
综上所述,原不等式成立 (16分)
考点:1.数列的递推关系;2.等差,等比数列的前n项和;3.不等式的证明

练习册系列答案
相关题目
 ,
, 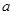 为实数,数列
为实数,数列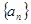 满足
满足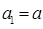 ,当
,当 时,
时,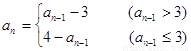
 时,求数列
时,求数列 ;
;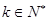 ,使
,使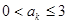 ;
;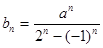 ,当
,当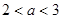 时,求证:
时,求证: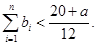
 ,若数列
,若数列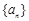 满足
满足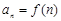 ,且
,且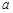 的取值范围为( )
的取值范围为( )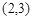 B.
B.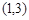 C.
C.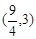 D.
D.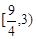
 满足
满足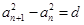 ,其中
,其中 为常数,则称数列
为常数,则称数列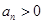 ,
,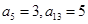 .
. 的前
的前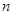 项和;
项和; ,则当实数
,则当实数 大于4时,不等式
大于4时,不等式 能否对于一切的
能否对于一切的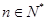 恒成立?请说明理由。
恒成立?请说明理由。