题目内容
已知点P为圆周x2+y2=4的动点,过P点作PH⊥x轴,垂足为H,设线段PH的中点为E,记点E的轨迹方程为C,点A(0,1)
(1)求动点E的轨迹方程C;
(2)若斜率为![]() 的另一个交点为B,求△OAB面积的最大值及此时直线l的方程;
的另一个交点为B,求△OAB面积的最大值及此时直线l的方程;
(3)是否存在方向向量![]() 的直线
的直线![]() 交与两个不同的点M,N,且有
交与两个不同的点M,N,且有![]() ?若存在,求出k的取值范围;若不存在,说明理由.
?若存在,求出k的取值范围;若不存在,说明理由.
答案:
解析:
解析:
|
(1)设 所以 (2) 而 此时,直线 (3)假设存在符合题设条件的直线 于是 而 故 故 可得: 由①②得: 故 |

练习册系列答案
相关题目


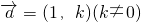 的直线l,使得l与曲线C交与两个不同的点M,N,且有
的直线l,使得l与曲线C交与两个不同的点M,N,且有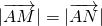 ?若存在,求出k的取值范围;若不存在,说明理由.
?若存在,求出k的取值范围;若不存在,说明理由. 的直线l,使得l与曲线C交与两个不同的点M,N,且有
的直线l,使得l与曲线C交与两个不同的点M,N,且有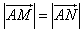 ?若存在,求出k的取值范围;若不存在,说明理由。
?若存在,求出k的取值范围;若不存在,说明理由。  的直线l,使得l与曲线C交与两个不同的点M,N,且有
的直线l,使得l与曲线C交与两个不同的点M,N,且有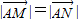 ?若存在,求出k的取值范围;若不存在,说明理由.
?若存在,求出k的取值范围;若不存在,说明理由.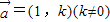 的直线l,使得l与曲线C交与两个不同的点M,N,且有
的直线l,使得l与曲线C交与两个不同的点M,N,且有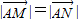 ?若存在,求出k的取值范围;若不存在,说明理由.
?若存在,求出k的取值范围;若不存在,说明理由.