题目内容
(Ⅰ)试比较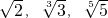 的大小;
的大小;
(Ⅱ)试比较nn+1与(n+1)n(n∈N+)的大小,根据(Ⅰ)的结果猜测一个一般性结论,并加以证明.
解:(Ⅰ)由于 ,
, ,则
,则
又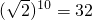 ,
, ,则
,则
所以
(Ⅱ)猜想:当n=1,2时,有nn+1<(n+1)n ; 当n≥3时,有nn+1>(n+1)n
证明如下:①当n=1时,不等式可化为:1<2,显然成立
当n=2时,不等式可化为:23<32,显然成立
②当n≥3时
设 ,
,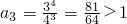
又
∴an+1>an,即数列{an}是一个单调递增数列
则an>an-1>…>a3>1
∴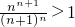 即nn+1>(n+1)n
即nn+1>(n+1)n
综上所述,当n=1、2时,有nn+1<(n+1)n
当n≥3时,nn+!>(n+1)n
分析:(1)用指数运算把根式化成整数后再比较大小
(2)给n赋值,计算结果,从而得到猜想,然后再用作商法证明猜想
点评:本题考查比较大小,间接考查指数运算和归纳推理.比较两个数的大小,最基本的方法是作差或作商.属简单题
 ,
, ,则
,则
又
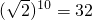 ,
, ,则
,则
所以

(Ⅱ)猜想:当n=1,2时,有nn+1<(n+1)n ; 当n≥3时,有nn+1>(n+1)n
证明如下:①当n=1时,不等式可化为:1<2,显然成立
当n=2时,不等式可化为:23<32,显然成立
②当n≥3时
设
 ,
,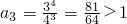
又

∴an+1>an,即数列{an}是一个单调递增数列
则an>an-1>…>a3>1
∴
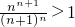 即nn+1>(n+1)n
即nn+1>(n+1)n综上所述,当n=1、2时,有nn+1<(n+1)n
当n≥3时,nn+!>(n+1)n
分析:(1)用指数运算把根式化成整数后再比较大小
(2)给n赋值,计算结果,从而得到猜想,然后再用作商法证明猜想
点评:本题考查比较大小,间接考查指数运算和归纳推理.比较两个数的大小,最基本的方法是作差或作商.属简单题

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
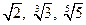 的大小;
的大小;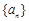 是等比数列,
是等比数列,  ,
, 是等差数列,
是等差数列,

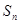 ;
; ,
,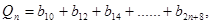 其中n=1,2,......,试比较
其中n=1,2,......,试比较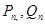 的大小。
的大小。 的公差
的公差 大于0,且
大于0,且 是方程
是方程 的两根,数列
的两根,数列 的前
的前 项和为
项和为 ,且
,且
 ,试比较
,试比较
 的大小,并说明理由.
的大小,并说明理由. 是首项
是首项 的等差数列,其前n项和为
的等差数列,其前n项和为 ,
, 是首项
是首项 的等比数列,且
的等比数列,且

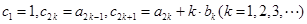 ,若数列
,若数列 的前n项和为
的前n项和为 ,试比较
,试比较 的大小。
的大小。