题目内容
已知复数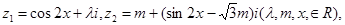 ,且
,且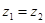 。
。
(Ⅰ)若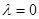 时,且
时,且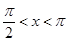 ,求x的值;
,求x的值;
(Ⅱ)设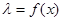 ,求
,求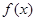 的单调递增区间。
的单调递增区间。
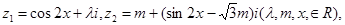 ,且
,且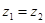 。
。(Ⅰ)若
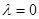 时,且
时,且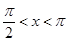 ,求x的值;
,求x的值;(Ⅱ)设
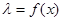 ,求
,求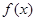 的单调递增区间。
的单调递增区间。(Ⅰ) (Ⅱ)
(Ⅱ)
 (Ⅱ)
(Ⅱ)
本试题主要是以复数为背景来分析三角方程的求解和三角函数的单调性的运用。
(1)因为利用复数相等,将其化为单一三角函数,解方程得到结论。
(2)由于正弦函数的增区间可知,那么代入之后得到其结论。
解:(Ⅰ) , 2分
, 2分
所以 3分
3分
又 ,所以
,所以 ; 4分
; 4分
(Ⅱ)由 6分
6分
得 , 7分
, 7分
递增区间为 。 8分
。 8分
(1)因为利用复数相等,将其化为单一三角函数,解方程得到结论。
(2)由于正弦函数的增区间可知,那么代入之后得到其结论。
解:(Ⅰ)
 , 2分
, 2分所以
 3分
3分又
 ,所以
,所以 ; 4分
; 4分(Ⅱ)由
 6分
6分得
 , 7分
, 7分递增区间为
 。 8分
。 8分 
练习册系列答案
相关题目
 (
( ,
, )为偶函数,且函数
)为偶函数,且函数 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为 .
. 的值;
的值;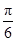 个单位后,得到函数
个单位后,得到函数 的图象,求
的图象,求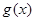 的单调递减区间.
的单调递减区间.  的一部分图象如图,那么
的一部分图象如图,那么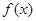 的解析式以及
的解析式以及
 的值分别是( )
的值分别是( )
 ,
, 
 ,
, 
 ,
,  ,
,  (
( )的图象如右图所示,为了得到
)的图象如右图所示,为了得到 的图象,可以将
的图象,可以将 的图象( )
的图象( )
 个单位长度
个单位长度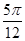 个单位长度
个单位长度 的角
的角 所对的边分别是
所对的边分别是 ,设向量
,设向量

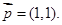
 求角B的大小;
求角B的大小; 边长c=2,角
边长c=2,角 求
求 ,有下列命题:
,有下列命题: ,且
,且 ;
;  对称;
对称;  求得 。
求得 。 作怎样的变换可得到函数
作怎样的变换可得到函数 ( )
( ) 个单位
个单位  个单位
个单位  的图象,只要将函数
的图象,只要将函数 的图象( )
的图象( )  单位
单位 单位
单位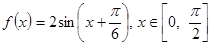 ,则该函数的值域为__________.
,则该函数的值域为__________.