题目内容
已知命题p: ;命题q:函数y=log2(x2-2kx+k)的值域为R,则p是q的 条件.
;命题q:函数y=log2(x2-2kx+k)的值域为R,则p是q的 条件.
【答案】分析:先利用绝对值不等式化简求出命题p: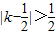 中k的范围;再把q进行转化,得出k的取值范围,函数y=log2(x2-2kx+k)的值域为R,即对应真数能取到所有的正数,即对应的方程的判别式△≥0.最后根据充要条件的定义进行判断.
中k的范围;再把q进行转化,得出k的取值范围,函数y=log2(x2-2kx+k)的值域为R,即对应真数能取到所有的正数,即对应的方程的判别式△≥0.最后根据充要条件的定义进行判断.
解答:解:命题p: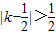 ,
,
∴k>1或k<0,
命题q:函数y=log2(x2-2kx+k)的值域为R,说明(x2-2kx+k)取遍正实数,
即△≥0,4k2-4k≥0,
∴k≥1或k≤0,
所以命题P⇒命题q,反之不成立.
故答案为:充分不必要.
点评:本题考查充分必要条件的判断方法,把命题p、q中k的取值范围求出来是关键.
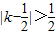 中k的范围;再把q进行转化,得出k的取值范围,函数y=log2(x2-2kx+k)的值域为R,即对应真数能取到所有的正数,即对应的方程的判别式△≥0.最后根据充要条件的定义进行判断.
中k的范围;再把q进行转化,得出k的取值范围,函数y=log2(x2-2kx+k)的值域为R,即对应真数能取到所有的正数,即对应的方程的判别式△≥0.最后根据充要条件的定义进行判断.解答:解:命题p:
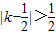 ,
,∴k>1或k<0,
命题q:函数y=log2(x2-2kx+k)的值域为R,说明(x2-2kx+k)取遍正实数,
即△≥0,4k2-4k≥0,
∴k≥1或k≤0,
所以命题P⇒命题q,反之不成立.
故答案为:充分不必要.
点评:本题考查充分必要条件的判断方法,把命题p、q中k的取值范围求出来是关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目