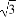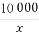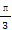Question

求下列各函数的导数:

(1)y=(x+1)(x+2)(x+3).

(2)y=+.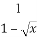

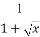(3)y=e-xsin2x.

 

Answer 1

(1) y'=3x2+12x+11 (2) y'=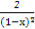. (3) y' =e-x(2cos2x-sin2x).

【解析】(1)方法一:y=(x2+3x+2)(x+3)=x3+6x2+11x+6,∴y'=3x2+12x+11.

方法二:y'=[(x+1)(x+2)]'(x+3)+(x+1)(x+2)·(x+3)'

=[(x+1)'(x+2)+(x+1)(x+2)'](x+3)+(x+1)·(x+2)

=(x+2+x+1)(x+3)+(x+1)(x+2)

=(2x+3)(x+3)+(x+1)(x+2)

=3x2+12x+11.

(2)∵y=+=,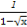

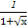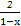∴y'=()'==.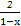

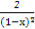(3)y'=(-e-x)sin2x+e-x(cos2x)×2

=e-x(2cos2x-sin2x).