题目内容
已知函数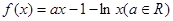
(1)当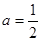 时,求函数在
时,求函数在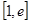 上的最大值和最小值;
上的最大值和最小值;
(2)讨论函数的单调性;
(3)若函数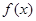 在
在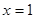 处取得极值,不等式
处取得极值,不等式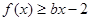 对
对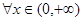 恒成立,求实数
恒成立,求实数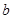 的取值范围。
的取值范围。
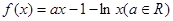
(1)当
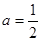 时,求函数在
时,求函数在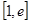 上的最大值和最小值;
上的最大值和最小值;(2)讨论函数的单调性;
(3)若函数
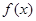 在
在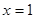 处取得极值,不等式
处取得极值,不等式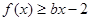 对
对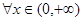 恒成立,求实数
恒成立,求实数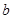 的取值范围。
的取值范围。(1)最大值是 ,最小值是
,最小值是 (2)当
(2)当 单调递减,在
单调递减,在 单调递增,当
单调递增,当 单调递减(3)
单调递减(3)
 ,最小值是
,最小值是 (2)当
(2)当 单调递减,在
单调递减,在 单调递增,当
单调递增,当 单调递减(3)
单调递减(3)
试题分析:解:(1)当

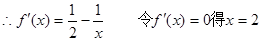
当



又
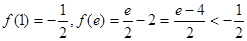
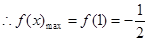
 上的最大值是
上的最大值是 ,最小值是
,最小值是 。
。(2)

当
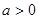 时,令
时,令 。
。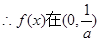 单调递减,在
单调递减,在 单调递增
单调递增当
 恒成立
恒成立  为减函数
为减函数当
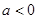 时,
时, 恒成立
恒成立  单调递减。
单调递减。综上,当
 单调递减,在
单调递减,在 单调递增,当
单调递增,当 单调递减
单调递减 (3)
 ,依题意:
,依题意:
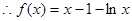
又
 恒成立。即
恒成立。即
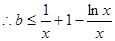 在
在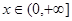 上恒成立
上恒成立令

当
 时
时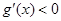 ,当
,当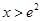 时
时 ,∴
,∴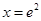 时
时 ,
, 
点评:求较复杂函数的性质,常用到导数。导数对求函数的单调区间、最值、不等式等问题都有很大作用。

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
 且
且 则
则 = ( )
= ( )



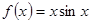 ,
,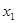 、
、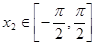 ,且
,且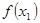 >
>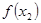 ,则下列结论必成立的是( )
,则下列结论必成立的是( )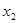
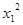 >
>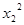
 在
在 上可导,且
上可导,且 ,
, __
__

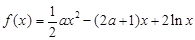 ,其中常数
,其中常数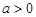 .
.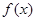 的单调区间;
的单调区间;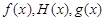 在公共定义域D上,满足
在公共定义域D上,满足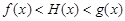 ,那么就称
,那么就称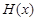 为
为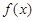 与
与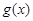 的“和谐函数”.设
的“和谐函数”.设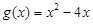 ,求证:当
,求证:当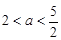 时,在区间
时,在区间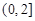 上,函数
上,函数 (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数. 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.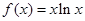 ,若
,若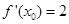 ,则
,则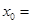 ( )
( )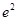
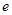
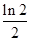
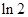
 ,
, 为f(x)的导函数,令a=- ,b=log32,则下列关系正确的是( )
为f(x)的导函数,令a=- ,b=log32,则下列关系正确的是( ) ,则
,则 ( )
( )


