题目内容
以点C(-4,3)为圆心的圆与直线2x+y-5=0相离,则圆C的半径R的取值范围是
- A.(0,20)
- B.(0,
 )
) - C.(0,2
 )
) - D.(0,10)
C
分析:依题意可知,圆心点C(-4,3)到直线2x+y-5=0的距离大于半径,从而可得答案.
解答:要使点C(-4,3)为圆心的圆与直线2x+y-5=0相离,
则圆心点C(-4,3)到直线2x+y-5=0的距离大于半径,
∵圆心点C(-4,3)到直线2x+y-5=0的距离d=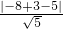 =2
=2 ,
,
∴R<2 ,又R>0,
,又R>0,
∴0<R<2 .
.
故选C.
点评:本题考查直线与圆的位置关系,考查点到直线间的距离公式,属于基础题.
分析:依题意可知,圆心点C(-4,3)到直线2x+y-5=0的距离大于半径,从而可得答案.
解答:要使点C(-4,3)为圆心的圆与直线2x+y-5=0相离,
则圆心点C(-4,3)到直线2x+y-5=0的距离大于半径,
∵圆心点C(-4,3)到直线2x+y-5=0的距离d=
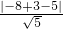 =2
=2 ,
,∴R<2
 ,又R>0,
,又R>0,∴0<R<2
 .
.故选C.
点评:本题考查直线与圆的位置关系,考查点到直线间的距离公式,属于基础题.

练习册系列答案
相关题目
 )
) )
)