��Ŀ����
�������У�1����2����3������ѡ���⣬ÿ��7�֣��뿼����ѡ2����������14�֡������������������ǰ����Ƿ֡�����ʱ������2BǦ���ڴ���ϰ���ѡ��Ŀ��Ӧ�����Ϳ�ڣ�������ѡ������������С�
��1������С������7�֣�ѡ��4-2��������任
��֪����M= ��N=
��N=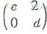 ����MN=
����MN=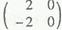 ��
��
������ʵ��a,b,c,d��ֵ��������ֱ��y=3x�ھ���M����Ӧ�����Ա任�����µ���ķ��̡�
��2������С������7�֣�ѡ��4-4������ϵ���������
��ֱ������ϵxOy�У�ֱ��L�IJ�������Ϊ ��tΪ���������ڼ�����ϵ����ֱ������ϵxOyȡ��ͬ�ij��ȵ�λ������ԭ��OΪ���㣬��x��������Ϊ���ᣩ�У�ԲC�ķ���Ϊ =2
=2 sin
sin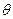 ��
��
������ԲC��ֱ�����귽�̣�
������ԲC��ֱ��L���ڵ�A,B������P������Ϊ��3��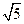 ������OPA�O+�OPB�O��
������OPA�O+�OPB�O��
��3������С������7�֣�ѡ��4-5������ʽѡ��
��֪����f(x)= �Ox-a�O.
����������ʽf(x)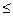 3�Ľ⼯Ϊ
3�Ľ⼯Ϊ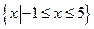 ����ʵ��a��ֵ��
����ʵ��a��ֵ��
�����ڣ��������£���f(x)+f(x+5)��m��һ��ʵ��x���������ʵ��m��ȡֵ��Χ��
��1������С������7�֣�ѡ��4-2��������任
��֪����M=
 ��N=
��N=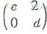 ����MN=
����MN=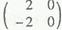 ��
��������ʵ��a,b,c,d��ֵ��������ֱ��y=3x�ھ���M����Ӧ�����Ա任�����µ���ķ��̡�
��2������С������7�֣�ѡ��4-4������ϵ���������
��ֱ������ϵxOy�У�ֱ��L�IJ�������Ϊ ��tΪ���������ڼ�����ϵ����ֱ������ϵxOyȡ��ͬ�ij��ȵ�λ������ԭ��OΪ���㣬��x��������Ϊ���ᣩ�У�ԲC�ķ���Ϊ
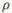 =2
=2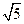 sin
sin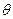 ��
��������ԲC��ֱ�����귽�̣�
������ԲC��ֱ��L���ڵ�A,B������P������Ϊ��3��
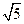 ������OPA�O+�OPB�O��
������OPA�O+�OPB�O����3������С������7�֣�ѡ��4-5������ʽѡ��
��֪����f(x)= �Ox-a�O.
����������ʽf(x)
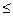 3�Ľ⼯Ϊ
3�Ľ⼯Ϊ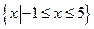 ����ʵ��a��ֵ��
����ʵ��a��ֵ�������ڣ��������£���f(x)+f(x+5)��m��һ��ʵ��x���������ʵ��m��ȡֵ��Χ��
��1��ѡ��4-2��������任
��С����Ҫ���������任�Ȼ���֪ʶ�����������������������7�֡�
�ⷨһ��
����������ã�
������Ϊ����MΪ��Ӧ�����Ա任��ֱ�߱��ֱ�ߣ���㣩�����Կ�ȡֱ��y=3x�ϵ����㣨0��0������1��3����
��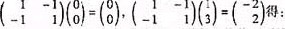
�㣨0��0������1��3���ھ���M����Ӧ�����Ա任�����µ����ǵ㣨0��0������-2��2��.
�Ӷ���ֱ��y=3x�ھ���M����Ӧ�����Ա任�����µ���ķ���Ϊy=-x��
�ⷨ����
����ͬ�ⷨһ��
������ֱ��y=3x�ϵ�����㣨x,y���ھ���M����Ӧ�����Ա任�����µ����ǵ㣨x��,y��������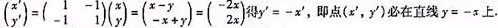
�ɣ�x,y���������Կ�֪��ֱ��y=3x�ھ���M����Ӧ�����Ա任�����µ���ķ���Ϊy= -x��
��2��ѡ��4-4������ϵ���������
��С����Ҫ����ֱ�ߵIJ������̡�Բ�ļ����귽�̡�ֱ����Բ��λ�ù�ϵ�Ȼ���֪ʶ�����������������������7�֡�
�ⷨһ��

������ʽ��t�ļ��������
�ⷨ����
����ͬ�ⷨһ��
������ΪԲC��Բ��Ϊ��0�� �����뾶r=
�����뾶r= ,ֱ��l����ͨ����Ϊ��y=-x+3+
,ֱ��l����ͨ����Ϊ��y=-x+3+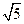 .
.
��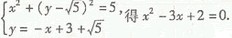 ��ã�
��ã� ��
��
������A��1��2+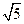 �� ��B��2��1+
�� ��B��2��1+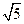 �����ֵ�P������Ϊ��3��
�����ֵ�P������Ϊ��3��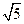 ����
����

����֪����ʽf(x)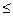 3�Ľ⼯Ϊ
3�Ľ⼯Ϊ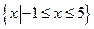 ������
������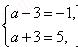 ���a=2.
���a=2.
����a=2ʱ��f(x)=�Ox-2�O.��g(x)=f(x)+f(x+5)������
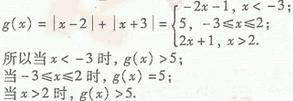
���Ͽɵã�g(x)����СֵΪ5.
�Ӷ�����f(x)+f(x+5)��m��g(x) ��m ��һ��ʵ��x ���������m��ȡֵ��ΧΪ(-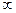 ��5].
��5].
�ⷨ����
����ͬ�ⷨһ��
����a=2ʱ��f(x)=�Ox-2�O.��g(x)=f(x)+f(x+5).
�ɨOx-2�O+�Ox+3�O�ݨO(x-2)-(x+3)�O="5" �����ҽ���-3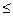 x
x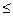 2ʱ�Ⱥų������ã�g(x)����СֵΪ5.
2ʱ�Ⱥų������ã�g(x)����СֵΪ5.
�Ӷ�����f(x)+f(x+5) ��m �� g(x) ��m��һ��ʵ��x���������m��ȡֵ��ΧΪ(-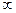 ��5].
��5].
��С����Ҫ���������任�Ȼ���֪ʶ�����������������������7�֡�
�ⷨһ��
����������ã�

������Ϊ����MΪ��Ӧ�����Ա任��ֱ�߱��ֱ�ߣ���㣩�����Կ�ȡֱ��y=3x�ϵ����㣨0��0������1��3����
��
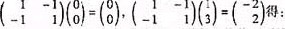
�㣨0��0������1��3���ھ���M����Ӧ�����Ա任�����µ����ǵ㣨0��0������-2��2��.
�Ӷ���ֱ��y=3x�ھ���M����Ӧ�����Ա任�����µ���ķ���Ϊy=-x��
�ⷨ����
����ͬ�ⷨһ��
������ֱ��y=3x�ϵ�����㣨x,y���ھ���M����Ӧ�����Ա任�����µ����ǵ㣨x��,y��������
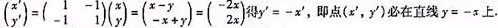
�ɣ�x,y���������Կ�֪��ֱ��y=3x�ھ���M����Ӧ�����Ա任�����µ���ķ���Ϊy= -x��
��2��ѡ��4-4������ϵ���������
��С����Ҫ����ֱ�ߵIJ������̡�Բ�ļ����귽�̡�ֱ����Բ��λ�ù�ϵ�Ȼ���֪ʶ�����������������������7�֡�
�ⷨһ��

������ʽ��t�ļ��������

�ⷨ����
����ͬ�ⷨһ��
������ΪԲC��Բ��Ϊ��0��
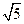 �����뾶r=
�����뾶r=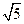 ,ֱ��l����ͨ����Ϊ��y=-x+3+
,ֱ��l����ͨ����Ϊ��y=-x+3+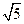 .
.��
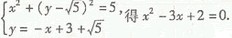 ��ã�
��ã� ��
��
������A��1��2+
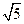 �� ��B��2��1+
�� ��B��2��1+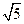 �����ֵ�P������Ϊ��3��
�����ֵ�P������Ϊ��3��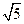 ����
����
����֪����ʽf(x)
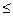 3�Ľ⼯Ϊ
3�Ľ⼯Ϊ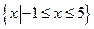 ������
������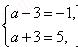 ���a=2.
���a=2.����a=2ʱ��f(x)=�Ox-2�O.��g(x)=f(x)+f(x+5)������
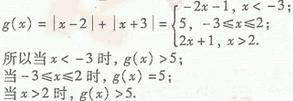
���Ͽɵã�g(x)����СֵΪ5.
�Ӷ�����f(x)+f(x+5)��m��g(x) ��m ��һ��ʵ��x ���������m��ȡֵ��ΧΪ(-
 ��5].
��5].�ⷨ����
����ͬ�ⷨһ��
����a=2ʱ��f(x)=�Ox-2�O.��g(x)=f(x)+f(x+5).
�ɨOx-2�O+�Ox+3�O�ݨO(x-2)-(x+3)�O="5" �����ҽ���-3
 x
x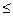 2ʱ�Ⱥų������ã�g(x)����СֵΪ5.
2ʱ�Ⱥų������ã�g(x)����СֵΪ5.�Ӷ�����f(x)+f(x+5) ��m �� g(x) ��m��һ��ʵ��x���������m��ȡֵ��ΧΪ(-
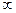 ��5].
��5].��

��ϰ��ϵ�д�
�����Ŀ
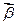 =
=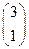 ���任T�ľ���ΪA=
���任T�ľ���ΪA=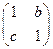 ��ƽ���ϵĵ�P��1��1���ڱ任T
��ƽ���ϵĵ�P��1��1���ڱ任T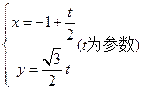 ��Բ
��Բ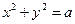 ��
�� >0���ཻ��A��B���㣬��
>0���ཻ��A��B���㣬��
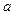 2+
2+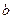 2�����������2
2�����������2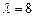 ����Ӧ��һ����������
����Ӧ��һ����������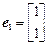 �����Ҿ���M��Ӧ�ı任����
�����Ҿ���M��Ӧ�ı任���� �任��
�任�� ��
�� �ھ���M�������µ�ֱ��
�ھ���M�������µ�ֱ��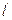 �ķ��̣�
�ķ��̣� 1=4����Ӧ��һ����������e1=
1=4����Ӧ��һ����������e1= ����������ֵ
����������ֵ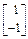 .
.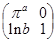 �ǵ�λ������
�ǵ�λ������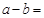 .
. 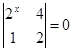 ����
����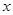 =__________
=__________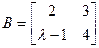 ����
����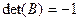 ,��
,�� =
= 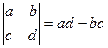 ����ʽ
����ʽ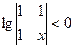 �Ľ⼯��
�Ľ⼯��