题目内容
已知函数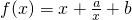 ,(x>0),其中a,b∈R.
,(x>0),其中a,b∈R.
(1)讨论函数f(x)的单调性(不必证明);
(2)当 时,不等式f(x)≤10在
时,不等式f(x)≤10在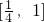 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.
解:(1)当a<0时,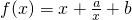 ,在(0,+∞)上是增函数;
,在(0,+∞)上是增函数;
当a=0时,f(x)=x+b,在(0,+∞)上是增函数;
当a>0时,f(x)在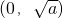 上是减函数,在
上是减函数,在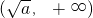 上是增函数.
上是增函数.
(2)不等式f(x)≤10在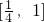 上恒成立,即等价于f(x)max≤10在
上恒成立,即等价于f(x)max≤10在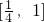 上恒成立
上恒成立
 ,f(1)=1+a+b
,f(1)=1+a+b
因为 ,所以
,所以 =
= >0
>0
所以 ,
,
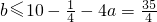 ,
,
即
分析:(1)对参数a进行讨论.当a<0时,在(0,+∞)上是增函数;当a=0,时f(x)=x+b,在(0,+∞)上是增函数;
当a>0,时f(x)在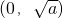 上是减函数,在
上是减函数,在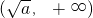 上是增函数.
上是增函数.
(2)不等式f(x)≤10在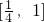 上恒成立,即等价于f(x)max≤10在
上恒成立,即等价于f(x)max≤10在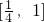 上恒成立,由于函数在
上恒成立,由于函数在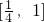 上的最大值在
上的最大值在 ,1上取得,故只需比较
,1上取得,故只需比较 ,f(1)=1+a+b即可,从而可求b的取值范围.
,f(1)=1+a+b即可,从而可求b的取值范围.
点评:本题的考点是函数恒成立问题,主要考查函数的单调性,考查利用函数的最值求解函数恒成立问题,关键是分类讨论,确定函数再区间上的最大值.
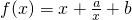 ,在(0,+∞)上是增函数;
,在(0,+∞)上是增函数;当a=0时,f(x)=x+b,在(0,+∞)上是增函数;
当a>0时,f(x)在
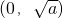 上是减函数,在
上是减函数,在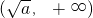 上是增函数.
上是增函数.(2)不等式f(x)≤10在
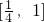 上恒成立,即等价于f(x)max≤10在
上恒成立,即等价于f(x)max≤10在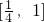 上恒成立
上恒成立 ,f(1)=1+a+b
,f(1)=1+a+b因为
 ,所以
,所以 =
= >0
>0所以
 ,
,
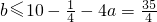 ,
,即

分析:(1)对参数a进行讨论.当a<0时,在(0,+∞)上是增函数;当a=0,时f(x)=x+b,在(0,+∞)上是增函数;
当a>0,时f(x)在
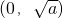 上是减函数,在
上是减函数,在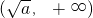 上是增函数.
上是增函数.(2)不等式f(x)≤10在
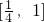 上恒成立,即等价于f(x)max≤10在
上恒成立,即等价于f(x)max≤10在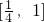 上恒成立,由于函数在
上恒成立,由于函数在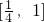 上的最大值在
上的最大值在 ,1上取得,故只需比较
,1上取得,故只需比较 ,f(1)=1+a+b即可,从而可求b的取值范围.
,f(1)=1+a+b即可,从而可求b的取值范围.点评:本题的考点是函数恒成立问题,主要考查函数的单调性,考查利用函数的最值求解函数恒成立问题,关键是分类讨论,确定函数再区间上的最大值.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 已知函数
已知函数