题目内容
我们知道，如果定义在某区间上的函数f（x）满足对该区间上的任意两个数x1、x2，总有不等式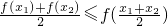
成立，则称函数f（x）为该区间上的向上凸函数（简称上凸）．类比上述定义，对于数列{an}，如果对任意正整数n，总有不等式：
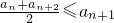成立，则称数列{an}为向上凸数列（简称上凸数列）．现有数列{an}满足如下两个条件：
（1）数列{an}为上凸数列，且a1=1，a10=28；
（2）对正整数n（1≤n＜10，n∈N*），都有|an-bn|≤20，其中bn=n2-6n+10．
则数列{an}中的第五项a5的取值范围为________．
解：∵，∴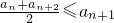
，
∴
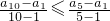，把a1=1，a10=28代入，得a5≥13…（1）．
在|an-bn|≤20，bn=n2-6n+10中，令n=5，得b5=25-30+10=5，
∴-20≤a5-b5≤20，∴-15≤a5≤25…（2）．
（1）、（2）联立得13≤a≤25．
答案：[13，25]．
分析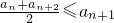：??a5≥13…（1），在|an-bn|≤20，bn=n2-6n+10中，令n=5?-15≤a5≤25…（2）；（1）、（2）联立能得到第五项a5的取值范围．
点评：本题具有一定的难度，解题时要注意公式的合理转化．
，∴，∴
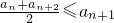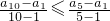，把a1=1，a10=28代入，得a5≥13…（1）．在|an-bn|≤20，bn=n2-6n+10中，令n=5，得b5=25-30+10=5，
∴-20≤a5-b5≤20，∴-15≤a5≤25…（2）．
（1）、（2）联立得13≤a≤25．
答案：[13，25]．
分析：
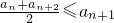??a5≥13…（1），在|an-bn|≤20，bn=n2-6n+10中，令n=5?-15≤a5≤25…（2）；（1）、（2）联立能得到第五项a5的取值范围．点评：本题具有一定的难度，解题时要注意公式的合理转化．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
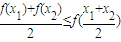成立，则称函数f（x）为该区间上的向上凸函数（简称上凸）．类比上述定义，对于数列{an}，如果对任意正整数n，总有不等式：
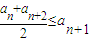成立，则称数列{an}为向上凸数列（简称上凸数列）．现有数列{an}满足如下两个条件：
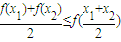成立，则称函数f（x）为该区间上的向上凸函数（简称上凸）．类比上述定义，对于数列{an}，如果对任意正整数n，总有不等式：
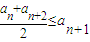成立，则称数列{an}为向上凸数列（简称上凸数列）．现有数列{an}满足如下两个条件：
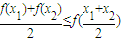成立，则称函数f（x）为该区间上的向上凸函数（简称上凸）．类比上述定义，对于数列{an}，如果对任意正整数n，总有不等式：
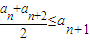成立，则称数列{an}为向上凸数列（简称上凸数列）．现有数列{an}满足如下两个条件：