题目内容
在极坐标系下,设圆C: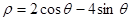 ,试求:
,试求:
(1)圆心的直角坐标表示
(2)在直角坐标系中,设曲线C经过变换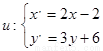 得到曲线
得到曲线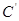 ,则曲线
,则曲线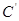 的轨迹是什么图形?
的轨迹是什么图形?
【答案】
(1)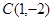 (2)轨迹是长轴长为
(2)轨迹是长轴长为 ,短轴长为
,短轴长为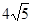 ,焦点在y轴的椭圆
,焦点在y轴的椭圆
【解析】
试题分析:(1)由圆C: ,左右同乘
,左右同乘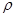 得
得
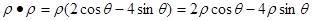
则 即
即
所以,圆心的坐标为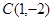
(2)由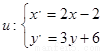 解得,
解得,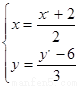 代入圆C的直坐标方程,解得
代入圆C的直坐标方程,解得
所以,它的轨迹是长轴长为 ,短轴长为
,短轴长为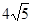 ,焦点在y轴的椭圆
,焦点在y轴的椭圆
考点:极坐标方程参数方程与普通方程的互化及轨迹方程的求解
点评:两坐标的互化:点的直角坐标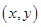 ,极坐标为
,极坐标为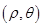 ,则
,则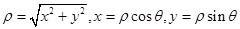
判断轨迹先求轨迹方程,相关点法求轨迹方程时转化出已知条件中的点后将其代入原方程化简

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
 [选做题]
[选做题] ,1),倾斜角
,1),倾斜角 ,在极坐标系下,圆C的极坐标方程为
,在极坐标系下,圆C的极坐标方程为 。
。 ,1),倾斜角
,1),倾斜角 ,在极坐标系下,圆C的极坐标方程为
,在极坐标系下,圆C的极坐标方程为 。
。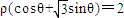 的距离为d,求d的最大值.
的距离为d,求d的最大值.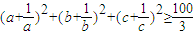 .
.