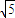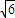题目内容
一条长为2的线段,它的三个视图分别是长为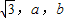 的三条线段,则ab的最大值为( )
的三条线段,则ab的最大值为( )A.
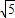
B.
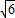
C.

D.3
【答案】分析:由棱和它在三视图中的投影扩展为长方体,三视图中的三个投影,是三个面对角线,设出三度,利用勾股定理,基本不等式求出最大值.
解答:解:将已知中的棱和它在三视图中的投影扩展为长方体,
三视图中的三个投影,是三个面对角线,
则设长方体的三度:x、y、z,
所以x2+y2+z2=4,x2+y2=a2,y2+z2=b2,x2+z2=3,
可解得a2+b2=5
∵ab≤ (a2+b2)=
(a2+b2)= ,当且仅当a=b时取等号,
,当且仅当a=b时取等号,
则ab的最大值为 .
.
故选C.
点评:本题考查三视图,几何体的结构特征,考查空间想象能力,基本不等式的应用,是中档题.
解答:解:将已知中的棱和它在三视图中的投影扩展为长方体,
三视图中的三个投影,是三个面对角线,
则设长方体的三度:x、y、z,
所以x2+y2+z2=4,x2+y2=a2,y2+z2=b2,x2+z2=3,
可解得a2+b2=5
∵ab≤
 (a2+b2)=
(a2+b2)= ,当且仅当a=b时取等号,
,当且仅当a=b时取等号,则ab的最大值为
 .
.故选C.
点评:本题考查三视图,几何体的结构特征,考查空间想象能力,基本不等式的应用,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
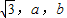 的三条线段,则ab的最大值为( )
的三条线段,则ab的最大值为( )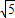
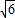

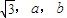 的三条线段,则ab的最大值为( )
的三条线段,则ab的最大值为( )