题目内容
1.已知l,m,n都是自然数,“l+m+n为偶数”是“l、m、n都是偶数”的什么条件?为什么?分析 根据充分必要条件的定义分别判断充分性和必要性即可.
解答 解:l+m+n为偶数”是“l、m、n都是偶数”的必要不充分条件.
因为由l+m+n为偶数不能推出l、m、n都是偶数(比如6=1+2+3)
由l、m、n都是偶数可以推出l+m+n为偶数
因为设l=2k1,m=2k2,n=2k3(k1,k2,k3都是整数)
显然l+m+n=2(k1+k2+k3)也是偶数.
点评 本题考查了充分必要条件,考查偶数问题,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.定义在R上的函数f(x)=$\left\{\begin{array}{l}{{2}^{x},x≤0}\\{f(x-1)-f(x-2),x>0}\end{array}\right.$,则f(3)的值为( )
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
11.下列函数中,是偶函数的是( )
| A. | f(x)=ex | B. | f(x)=log2x | C. | f(x)=|x| | D. | f(x)=x+1 |
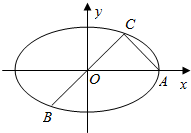 如图所示,已知A、B、C是长轴为4的椭圆E上的三点,点A是长轴的一个端点,BC过椭圆中心O,且AC⊥BC,|BC|=2|AC|.
如图所示,已知A、B、C是长轴为4的椭圆E上的三点,点A是长轴的一个端点,BC过椭圆中心O,且AC⊥BC,|BC|=2|AC|.