题目内容
本题有(1)、(2)、(3)三个选答题,每小题7分,请考生任选2题作答,满分14分,如果多做,则按所做的前两题计分.(1)选修4-2:矩阵与变换
已知矩阵A=
 .
.①求矩阵A的逆矩阵B;
②若直线l经过矩阵B变换后的方程为y=x,求直线l的方程.
(2)选修4-4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系中x轴的正半轴重合.圆C的参数方程为
 (a为参数),点Q极坐标为(2,
(a为参数),点Q极坐标为(2, π).
π).(Ⅰ)化圆C的参数方程为极坐标方程;
(Ⅱ)若点P是圆C上的任意一点,求P、Q两点距离的最小值.
(3)选修4-5:不等式选讲
(I)关于x的不等式|x-3|+|x-4|<a的解不是空集,求a的取值范围.
(II)设x,y,z∈R,且
 ,求x+y+z的取值范围.
,求x+y+z的取值范围.
【答案】分析:(1)①设矩阵A的逆矩阵B= ,由
,由
 =
= =
= ,求出B.
,求出B.
②由题意可得 =
=
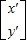 =
= ,且x′-y′=0.化简(-2x+y)-(
,且x′-y′=0.化简(-2x+y)-( -
- )=0,可得直线l的方程.
)=0,可得直线l的方程.
(2)(Ⅰ)把圆C的参数方程化为直角坐标方程为 (x-1)2+(y+1)2=4,再化为极坐标方程.
(Ⅱ)先求得点Q的直角坐标为( ,-
,- ),由于圆心C的坐标为(1-1),求得CQ=
),由于圆心C的坐标为(1-1),求得CQ=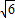 ,可得PQ的最小值为CQ-r,运算求得结果.
,可得PQ的最小值为CQ-r,运算求得结果.
(3)(I)由绝对值的意义可得,|x-3|+|x-4|的最小值为1,结合题意可得故a>1,从而求得a的取值范围.
(II)设x,y,z∈R,且 ,利用柯西不等式得 (x+y+z)2≤25,可得x+y+z的取值范围.
,利用柯西不等式得 (x+y+z)2≤25,可得x+y+z的取值范围.
解答:解:(1)①∵已知矩阵A=[ ],设矩阵A的逆矩阵B=
],设矩阵A的逆矩阵B=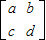 ,
,
则有
 =
= =
= .
.
∴ ,解得
,解得  ,故A的逆矩阵B=
,故A的逆矩阵B= .
.
②若直线l经过矩阵B变换后的方程为y=x,即x-y=0,
则 =
=
 =
= ,且x′-y′=0.
,且x′-y′=0.
∴(-2x+y)-( -
- )=0,即 7x-3y=0,∴直线l的方程为 7x-3y=0.
)=0,即 7x-3y=0,∴直线l的方程为 7x-3y=0.
(2)(Ⅰ)∵圆C的参数方程为 ,化为直角坐标方程为 (x-1)2+(y+1)2=4.
,化为直角坐标方程为 (x-1)2+(y+1)2=4.
再化为极坐标方程为 (ρcosθ-1)2+(ρsinθ+1)2=4.
(Ⅱ)∵点Q极坐标为(2, π),故点Q的直角坐标为(
π),故点Q的直角坐标为( ,-
,- ).
).
由于圆心C的坐标为(1-1),且CQ= =
= ,点P是圆C上的任意一点,
,点P是圆C上的任意一点,
故PQ的最小值为 CQ-r= -1.
-1.
(3)(I)关于x的不等式|x-3|+|x-4|<a的解不是空集,而由绝对值的意义可得,|x-3|+|x-4|的最小值为1,
故a>1,故a的取值范围为(1,+∞).
(II)设x,y,z∈R,且 ,利用柯西不等式得
,利用柯西不等式得
(16+5+4)×( )≥(x+y+z)2,
)≥(x+y+z)2,
∴(x+y+z)2≤25,
即-5≤x+y+z≤5,故x+y+z的取值范围为[-5,5].
点评:本题考查逆变换与逆矩阵,绝对值不等式的解法,柯西不等式的应用,参数方程、极坐标方程、以及直角坐标方程间的互化,属于中档题.
 ,由
,由
 =
= =
= ,求出B.
,求出B.②由题意可得
 =
=
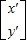 =
= ,且x′-y′=0.化简(-2x+y)-(
,且x′-y′=0.化简(-2x+y)-( -
- )=0,可得直线l的方程.
)=0,可得直线l的方程.(2)(Ⅰ)把圆C的参数方程化为直角坐标方程为 (x-1)2+(y+1)2=4,再化为极坐标方程.
(Ⅱ)先求得点Q的直角坐标为(
 ,-
,- ),由于圆心C的坐标为(1-1),求得CQ=
),由于圆心C的坐标为(1-1),求得CQ=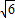 ,可得PQ的最小值为CQ-r,运算求得结果.
,可得PQ的最小值为CQ-r,运算求得结果.(3)(I)由绝对值的意义可得,|x-3|+|x-4|的最小值为1,结合题意可得故a>1,从而求得a的取值范围.
(II)设x,y,z∈R,且
 ,利用柯西不等式得 (x+y+z)2≤25,可得x+y+z的取值范围.
,利用柯西不等式得 (x+y+z)2≤25,可得x+y+z的取值范围.解答:解:(1)①∵已知矩阵A=[
 ],设矩阵A的逆矩阵B=
],设矩阵A的逆矩阵B=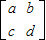 ,
,则有

 =
= =
= .
.∴
 ,解得
,解得  ,故A的逆矩阵B=
,故A的逆矩阵B= .
.②若直线l经过矩阵B变换后的方程为y=x,即x-y=0,
则
 =
=
 =
= ,且x′-y′=0.
,且x′-y′=0.∴(-2x+y)-(
 -
- )=0,即 7x-3y=0,∴直线l的方程为 7x-3y=0.
)=0,即 7x-3y=0,∴直线l的方程为 7x-3y=0.(2)(Ⅰ)∵圆C的参数方程为
 ,化为直角坐标方程为 (x-1)2+(y+1)2=4.
,化为直角坐标方程为 (x-1)2+(y+1)2=4.再化为极坐标方程为 (ρcosθ-1)2+(ρsinθ+1)2=4.
(Ⅱ)∵点Q极坐标为(2,
 π),故点Q的直角坐标为(
π),故点Q的直角坐标为( ,-
,- ).
).由于圆心C的坐标为(1-1),且CQ=
 =
= ,点P是圆C上的任意一点,
,点P是圆C上的任意一点,故PQ的最小值为 CQ-r=
 -1.
-1.(3)(I)关于x的不等式|x-3|+|x-4|<a的解不是空集,而由绝对值的意义可得,|x-3|+|x-4|的最小值为1,
故a>1,故a的取值范围为(1,+∞).
(II)设x,y,z∈R,且
 ,利用柯西不等式得
,利用柯西不等式得 (16+5+4)×(
 )≥(x+y+z)2,
)≥(x+y+z)2,∴(x+y+z)2≤25,
即-5≤x+y+z≤5,故x+y+z的取值范围为[-5,5].
点评:本题考查逆变换与逆矩阵,绝对值不等式的解法,柯西不等式的应用,参数方程、极坐标方程、以及直角坐标方程间的互化,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目