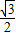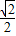题目内容
已知P是椭圆 上的一个动点,且P与椭圆长轴两个顶点连线的斜率之积为
上的一个动点,且P与椭圆长轴两个顶点连线的斜率之积为 ,则椭圆的离心率为( )
,则椭圆的离心率为( )A.

B.

C.

D.

【答案】分析:设点P的坐标为(x,y),根据椭圆长轴两个顶点坐标为(-a,0),(a,0),P与椭圆长轴两个顶点连线的斜率之积为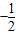 ,可得方程,再利用点P在椭圆上,即可求得椭圆的离心率.
,可得方程,再利用点P在椭圆上,即可求得椭圆的离心率.
解答:解:设点P的坐标为(x,y),则
∵椭圆长轴两个顶点坐标为(-a,0),(a,0),P与椭圆长轴两个顶点连线的斜率之积为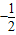 ,
,
∴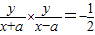
∴-2y2=x2-a2①
∵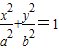
∴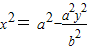 ②
②
由①②可得a2=2b2
∴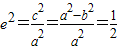
∴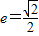
∴椭圆的离心率为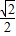
故选B.
点评:本题重点考查椭圆的离心率,解题的关键是利用P与椭圆长轴两个顶点连线的斜率之积为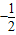 ,寻找几何量之间的关系.
,寻找几何量之间的关系.
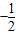 ,可得方程,再利用点P在椭圆上,即可求得椭圆的离心率.
,可得方程,再利用点P在椭圆上,即可求得椭圆的离心率.解答:解:设点P的坐标为(x,y),则
∵椭圆长轴两个顶点坐标为(-a,0),(a,0),P与椭圆长轴两个顶点连线的斜率之积为
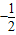 ,
,∴
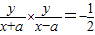
∴-2y2=x2-a2①
∵
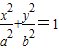
∴
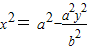 ②
②由①②可得a2=2b2
∴
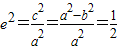
∴
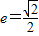
∴椭圆的离心率为
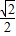
故选B.
点评:本题重点考查椭圆的离心率,解题的关键是利用P与椭圆长轴两个顶点连线的斜率之积为
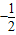 ,寻找几何量之间的关系.
,寻找几何量之间的关系. 
练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 上的一个动点,且P与椭圆长轴两个顶点连线的斜率之积为
上的一个动点,且P与椭圆长轴两个顶点连线的斜率之积为 ,则椭圆的离心率为( )
,则椭圆的离心率为( )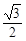 B.
B.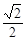 C.
C. D.
D.
 上的一个动点,且P与椭圆长轴两个顶点连线的斜率之积为
上的一个动点,且P与椭圆长轴两个顶点连线的斜率之积为 ,则椭圆的离心率为
,则椭圆的离心率为



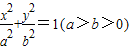 上的一个动点,且P与椭圆长轴两个顶点连线的斜率之积为
上的一个动点,且P与椭圆长轴两个顶点连线的斜率之积为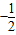 ,则椭圆的离心率为( )
,则椭圆的离心率为( )