题目内容
如果偶函数 ,当
,当 时,
时,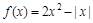 ,则
,则 在
在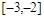 上是( )
上是( )
A.增函数,最大值为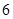 | B.增函数,最小值是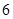 |
C.减函数,最大值为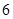 | D.减函数,最小值是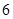 |
D
解析试题分析:利用函数的偶函数的对称性,可知在对称区间上单调性相反,因此当 时,
时,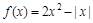 ,可知是
,可知是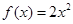 和
和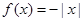 都是增函数,因此结合单调性的性质可知也是增函数,所以说明在
都是增函数,因此结合单调性的性质可知也是增函数,所以说明在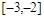 是减函数,因此有最小值f(-2)=f(2)=8-2=6,最大值f(-3)=f(3)=18-3=15,可知正确的选项为D.
是减函数,因此有最小值f(-2)=f(2)=8-2=6,最大值f(-3)=f(3)=18-3=15,可知正确的选项为D.
考点:本试题考查了函数的奇偶性和单调性的运用。
点评:解决该试题的关键是能利用函数单调性的性质:增+增=增,减-增=减,增-减=增
减+减=减,的思想来分析求解。同时要注意利用对称性进行-x和x函数值之间的对应即可,属于中档题。

练习册系列答案
 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
函数 的零点所在的区间为( )
的零点所在的区间为( )
A. | B. | C. | D. |
设函数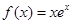 ,则( )
,则( )
A.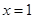 为 为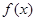 的极大值点 的极大值点 | B.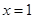 为 为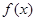 的极小值点 的极小值点 |
C.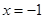 为 为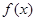 的极大值点 的极大值点 | D.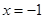 为 为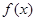 的极小值点 的极小值点 |
函数 在实数集上是增函数,则
在实数集上是增函数,则
A.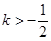 | B. | C. | D. |
设函数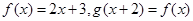 ,则
,则 的表达式是( )
的表达式是( )
A.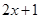 | B.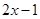 | C.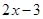 | D.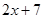 |
在区间 上不是增函数的是( )
上不是增函数的是( )
A. | B. | C. | D. |
为了求函数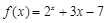 的一个零点,某同学利用计算器得到自变量
的一个零点,某同学利用计算器得到自变量 和函数
和函数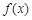 的部分对应值,如表所示:
的部分对应值,如表所示:
 | 1.25 | 1.3125 | 1.375 | 1.4375 | 1.5 | 1.5625 |
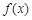 | -0.8716 | -0.5788 | -0.2813 | 0.2101 | 0.32843 | 0.64115 |
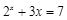 的近似解(精确到0.1)可取为
的近似解(精确到0.1)可取为(A)1.32 (B)1.39 (C)1.4 (D)1.3
下列说法正确的是
A.函数 在其定义域上是减函数 在其定义域上是减函数 |
| B.两个三角形全等是这两个三角形面积相等的必要条件 |
C.命题“ R, R, ”的否定是“ ”的否定是“  R, R, ” ” |
D.给定命题 、 、 ,若 ,若 是真命题,则 是真命题,则 是假命题 是假命题 |
 的图象大致是 ( )
的图象大致是 ( )