题目内容
(普通班)函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为( )
A.(-1,1) B.(-1,+∞) C.(-∞,-1) D.(-∞,+∞)
(实验班)已知可导函数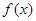 的导函数为
的导函数为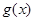 ,且满足:①
,且满足:①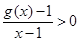 ,②
,②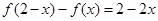 ,记
,记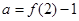 ,
,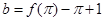 ,
,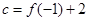 ,则
,则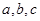 的大小顺序为( )
的大小顺序为( )
A.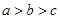 B.
B. 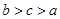 C.
C. 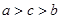 D.
D. 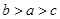
A.(-1,1) B.(-1,+∞) C.(-∞,-1) D.(-∞,+∞)
(实验班)已知可导函数
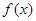 的导函数为
的导函数为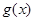 ,且满足:①
,且满足:①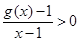 ,②
,②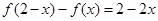 ,记
,记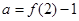 ,
,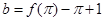 ,
,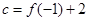 ,则
,则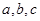 的大小顺序为( )
的大小顺序为( )A.
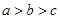 B.
B. 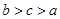 C.
C. 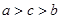 D.
D. 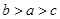
B
(普通班)令F(x)=f(x)-2x-4,则F(-1)="f(-1)-2x(-1)-4=0," F’(x)="f" ’(x)-2,
对任意x∈R f ’(x)>2,所以F’(x)>0,即F(x)在R上递增,所以F(x)>0时,x>-1
即f(x)>2x+4 解集为x>-1
(实验班)g(x)是f(x)的导函数,则g(x)-1就是f(x)-x的导函数
因g(x)-1/x-1>0故g(x)-1>1/x
当x>0时,由于1/x>0所以g(x)-1>0
所以f(x)-x在x>0时是增函数
令f(x)-x="h(x)" 则h(x)在x>0时是增函数
因f(2-x)-f(x)="2-2x" 令x=-1得f(3)-f(-1)=4即f(-1)=f(3)-4
a=f(2)-1=f(2)-2+1=h(2)+1
b=f(π)-π+1=h(π)+1
c= f(-1)+2=f(3)-4+2=f(3)-3+1=h(3)+1
因2<3<π 由h(x)的单调性可知h(2)<h(3)<h(π)
所以a<c<b
对任意x∈R f ’(x)>2,所以F’(x)>0,即F(x)在R上递增,所以F(x)>0时,x>-1
即f(x)>2x+4 解集为x>-1
(实验班)g(x)是f(x)的导函数,则g(x)-1就是f(x)-x的导函数
因g(x)-1/x-1>0故g(x)-1>1/x
当x>0时,由于1/x>0所以g(x)-1>0
所以f(x)-x在x>0时是增函数
令f(x)-x="h(x)" 则h(x)在x>0时是增函数
因f(2-x)-f(x)="2-2x" 令x=-1得f(3)-f(-1)=4即f(-1)=f(3)-4
a=f(2)-1=f(2)-2+1=h(2)+1
b=f(π)-π+1=h(π)+1
c= f(-1)+2=f(3)-4+2=f(3)-3+1=h(3)+1
因2<3<π 由h(x)的单调性可知h(2)<h(3)<h(π)
所以a<c<b

练习册系列答案
相关题目
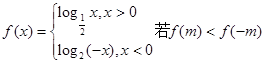 ,则实数m的取值范围是()
,则实数m的取值范围是()



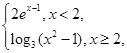
 则不等式f(x)>2的解集为 。
则不等式f(x)>2的解集为 。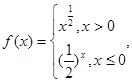 则
则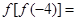 ( )
( )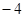

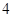
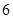
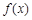 的定义域是R,对于任意实数
的定义域是R,对于任意实数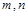 ,恒有
,恒有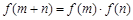 ,且当
,且当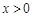 时,
时,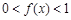 .
.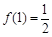 ,求
,求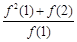 的值;(Ⅱ)求证:
的值;(Ⅱ)求证: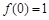 ,且当
,且当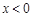 时,有
时,有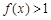 ;
;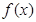 是定义在
是定义在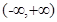 上的奇函数,若对于任意的实数
上的奇函数,若对于任意的实数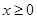 ,都有
,都有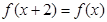 ,且当
,且当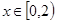 时,
时,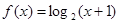 ,则
,则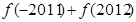 的值为( )
的值为( )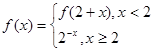 ,则
,则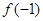 的值为
的值为 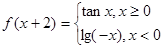 ,则
,则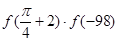 等于
等于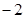
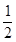
 上的函数
上的函数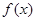 满足
满足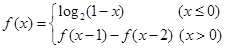 ,则
,则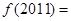 ( )
( )