题目内容

已知双曲线
x2
4
-
y2
a
=1的实轴为A1A2，虚轴为B1B2，将坐标系的右半平面沿y轴折起，使双曲线的右焦点F2折至点F，若点F在平面A1B1B2内的射影恰好是该双曲线的左顶点A1，且直线B1F与平面A1B1B2所成角的正切值为
5
5
，则a=
1
1
．
分析：由题意可得直线B1F与平面A1B1B2所成角为∠FB1A1，可得
5
5
=
FA1
A1B1
=
FA1
4+a
，求得 FA1 的值，
直角三角形FA1O 中，由勾股定理可得 FO2=A1O2+FA12，由此求出a 的值．
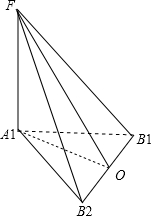
解答：解：如图所示：由题意可得 实轴A1A2 =4，B1B2，=2
a
，FA1⊥面A1B1B2，
直线B1F与平面A1B1B2所成角为∠FB1A1．
∴
5
5
=
FA1
A1B1
=
FA1
4+a
，∴FA1=
5
5
4+a
．
又FO=c=
4+a
，A1O=2．直角三角形FA1O 中，由勾股定理可得 FO2=A1O2+FA12，
即4+a=4+
4+a
5
，解得 a=1．
故答案为：1．
点评：本题考查双曲线的标准方程，以及双曲线的简单性质，直线和平面所成的角，体现了数形结合的数学思想，属于
中档题．
练习册系列答案
相关题目
给出下列四个结论：
①当a为任意实数时，直线（a-1）x-y+2a+1=0恒过定点P，则过点P且焦点在y轴上的抛物线的标准方程是x2=
4
3
y；
②已知双曲线的右焦点为（5，0），一条渐近线方程为2x-y=0，则双曲线的标准方程是
x2
5
-
y2
20
=1；
③抛物线y=ax2(a≠0)的准线方程为y=-
1
4a
；
④已知双曲线
x2
4
+
y2
m
=1，其离心率e∈（1，2），则m的取值范围是（-12，0）．
其中所有正确结论的个数是（　　）
（2008•佛山一模）已知双曲线
x2
4
-y2=1，则其渐近线方程为
y=±
1
2
x
y=±
1
2
x
，离心率为
5
2
5
2
．
（2011•焦作一模）已知双曲线
x2
4
-
y2
12
=1的离心率为e，焦点为F的抛物线y2=2px与直线y=k（x-
p
2
）交于A、B两点，且
|AF|
|FB|
=e，则k的值为
+
.
2
2
+
.
2
2
．
给出下列四个结论：
①若α、β为锐角，tan（α+β）=-3，tanβ=
1
2
，则α+2β=
3π
4
；
②在△ABC中，若
AB
•
BC
＞0，则△ABC一定是钝角三角形；
③已知双曲线
x2
4
+
y2
m
=1，其离心率e∈（1，2），则m的取值范围是（-12，0）；
④当a为任意实数时，直线（a-1）x-y+2a+1=0恒过定点P，则焦点在y轴上且过点P的抛物线的标准方程是x2=
4
3
y．其中所有正确结论的个数是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网