题目内容
已知数列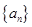 的前
的前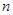 项和为
项和为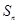 ,并且满足
,并且满足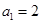 ,
,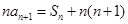 .
.
(1)求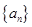 的通项公式;
的通项公式;
(2)令 ,问是否存在正整数
,问是否存在正整数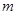 ,对一切正整数
,对一切正整数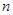 ,总有
,总有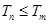 ?若存在,求出的值,若不存在,说明理由.
?若存在,求出的值,若不存在,说明理由.
【答案】
解:(1)令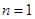 ,由
,由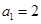 及
及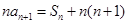 ①,得
①,得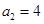 ,故
,故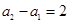 ,…2分
,…2分
当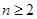 时,有
时,有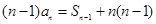 ②,②-①得
②,②-①得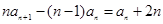 ,
,
整理得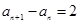 ,
…………………………………5分
,
…………………………………5分
当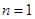 时,
时,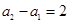 ,所以数列
,所以数列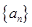 是以2为首项,以2为公差的等差数列,
是以2为首项,以2为公差的等差数列,
故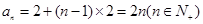 ;
…………………………………7分
;
…………………………………7分
(2)由(1)得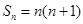 ,所以
,所以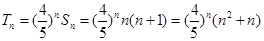 ,
,
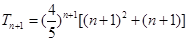 ,
…………………………………9分
,
…………………………………9分
令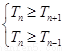 ,即
,即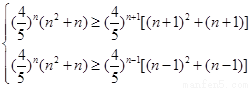 ,
……………………10分
,
……………………10分
即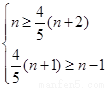 ,解得
,解得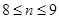 ,
…………………………………12分
,
…………………………………12分
故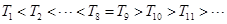 ,故存在正整数
,故存在正整数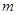 对一切正整数
对一切正整数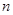 ,总有
,总有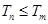 ,此时
,此时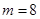 或
或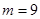 .
…………………………………14分
.
…………………………………14分
【解析】略

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
 的前
的前 项和为
项和为 ,满足
,满足 .
. 为等比数列,并
为等比数列,并 求出
求出 ;
; ,求
,求 的最大项.
的最大项. }的前
}的前 项和为
项和为 ,且
,且 (
( );
); =3
=3 (
(


 ;
; }的通项公式
}的通项公式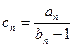 ,求数列
,求数列 的前
的前 .
. 的前
的前 项和为
项和为 ,且
,且 .
.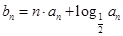 ,数列
,数列 的前
的前 ,若不等式
,若不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.