已知f(x)=.在区间[0,2]上任取三个数,均存在以为边长的三角形.则的取值范围是( )A．B．C．D．题目和参考答案——青夏教育精英家教网—

题目内容

已知f(x)=，在区间[0,2]上任取三个数,均存在以为边长的三角形，则的取值范围是（）

A．

B．

C．

D．

解析试题分析：因为函数=的导数为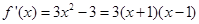，所以可知函数递减，递增.所以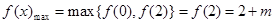，.又因为在区间[0,2]上任取三个数,均存在以为边长的三角形，等价于函数满足即.故选C.
考点：1.函数的最值.2.三角形的存在条件.3.三角形的存在性转化为函数的最值问题.

练习册系列答案

全能达标100分系列答案

相关题目

函数的反函数是（）

A．．	B．．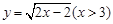
C．．	D．．

函数的定义域为（）

A．	B．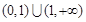
C．	D．

已知函数在时取得最大值，在时取得最小值，则实数的取值范围是（）

函数f(x)＝的定义域为________．

已知函数y＝f(x)是定义在R上的奇函数，且当x<0时，不等式f(x)＋xf′(x)<0成立，若a＝3^0.3f(3^0.3)，b＝log_π3f(log_π3)，c＝log₃f，则a，b，c间的大小关系是(　　)．

A．a>b>c	B．c>b>a
C．c>a>b	D．a>c>b

若函数y＝f(x)(x∈R)满足f(x＋1)＝－f(x)，且x∈[－1,1]时f(x)＝1－x².函数g(x)＝则函数h(x)＝f(x)－g(x)在区间[－5,4]内的零点的个数(　　)．

A．7	B．8?，
C．9	D．10

函数f(x)的定义域为R，f(－1)＝2，对任意x∈R，f′(x)>2，则f(x)>2x＋4的解集为(　　)．

A．(－1,1)	B．(－1，＋∞)
C．(－∞，－1)	D．(－∞，＋∞)

若曲线f(x，y)＝0上两个不同点处的切线重合，则称这条切线为曲线f(x，y)＝0的“自公切线”．下列方程：①x²－y²＝1；②y＝x²－|x|，③y＝3sin x＋4cos x；④|x|＋1＝对应的曲线中存在“自公切线”的有(　　)．

试题分类