题目内容
已知f(x)=lg(x2-mx+2m-1),m∈R
(Ⅰ)当m=0时,求f(x)的单调递增区间;
(Ⅱ)若函数f(x)的值域是[lg2,+∞),求m的值;
(Ⅲ)若x∈[0,1]时不等式f(x)>0恒成立,求实数m的取值范围.
(Ⅰ)当m=0时,求f(x)的单调递增区间;
(Ⅱ)若函数f(x)的值域是[lg2,+∞),求m的值;
(Ⅲ)若x∈[0,1]时不等式f(x)>0恒成立,求实数m的取值范围.
分析:(Ⅰ)利用复合函数的单调性去求函数的增区间.(Ⅱ)利用函数的值域是[lg2,+∞),确定m的数值.
(Ⅲ)不等式f(x)>0恒成立,实质是求当x∈[0,1]时,函数f(x)的最值.
(Ⅲ)不等式f(x)>0恒成立,实质是求当x∈[0,1]时,函数f(x)的最值.
解答:解:(Ⅰ)当m=0时,f(x)=lg(x2-1),设t=x2-1,
当x∈(1,+∞)时,t=x2-1递增,而当t>0时,y=lgt递增
所以f(x)的递增区间是(1,+∞)…(4分)
(Ⅱ)因为函数f(x)的值域是[lg2,+∞),依题意得t=x2-mx+2m-1的最小值是2,
解-
+2m-1=2得m=2或m=6…(8分)
(Ⅲ)法一:当x∈[0,1]时,将x2-mx+2m-2>0分离变量后得到
<m
令g(x)=
,则g′(x)=
,
令g′(x)=0得x=2±
…(11分)∴当0<x<2-
时g′(x)>0,当2-
<x<1时g′(x)<0
而x=2-
时取得最大值4-2
,∴m>4-2
…(14分)
法二:依题意得:x2-mx+2m-2>0,令h(x)=x2-mx+2m-2,轴是x=
(1)当
≤0时,则有f(0)=2m-2>0,解得m∈Φ;
(2)当0<
≤1时,则有△=m2-8m+8>0,解得4-2
<m≤2;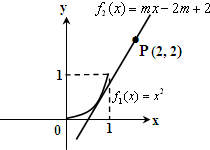
(3)当1<
时,则有f(1)=m-1>0,解得m>2
综上所求,实数m的取值范围是(4-2
,+∞)
法三:将x2-mx+2m-2>0移项得x2>mx-2m+2,设f1(x)=x2,f2(x)=mx-2m+2,
则f1(x)、f2(x)的图象分别为右图所示的一段抛物线和直线,要使对一切x∈[0,1],f1(x)>f2(x)恒成立,即要使得x∈[0,1]时,抛物线
段总在直线段的上方,因为直线恒过定点(2,2),可观察
图象得:直线的斜率必须大于相切时的斜率值,而相
切时的斜率可用判别式或导数易求得为4-2
,
所以m>4-2
.…(14分)
当x∈(1,+∞)时,t=x2-1递增,而当t>0时,y=lgt递增
所以f(x)的递增区间是(1,+∞)…(4分)
(Ⅱ)因为函数f(x)的值域是[lg2,+∞),依题意得t=x2-mx+2m-1的最小值是2,
解-
| m2 |
| 4 |
(Ⅲ)法一:当x∈[0,1]时,将x2-mx+2m-2>0分离变量后得到
| x2-2 |
| x-2 |
令g(x)=
| x2-2 |
| x-2 |
| x2-4x+2 |
| (x-2)2 |
令g′(x)=0得x=2±
| 2 |
| 2 |
| 2 |
而x=2-
| 2 |
| 2 |
| 2 |
法二:依题意得:x2-mx+2m-2>0,令h(x)=x2-mx+2m-2,轴是x=
| m |
| 2 |
(1)当
| m |
| 2 |
(2)当0<
| m |
| 2 |
| 2 |

(3)当1<
| m |
| 2 |
综上所求,实数m的取值范围是(4-2
| 2 |
法三:将x2-mx+2m-2>0移项得x2>mx-2m+2,设f1(x)=x2,f2(x)=mx-2m+2,
则f1(x)、f2(x)的图象分别为右图所示的一段抛物线和直线,要使对一切x∈[0,1],f1(x)>f2(x)恒成立,即要使得x∈[0,1]时,抛物线
段总在直线段的上方,因为直线恒过定点(2,2),可观察
图象得:直线的斜率必须大于相切时的斜率值,而相
切时的斜率可用判别式或导数易求得为4-2
| 2 |
所以m>4-2
| 2 |
点评:本题考查了与对数函数有关的复合函数的性质,对应复合函数可以通过换元法来进行转化.

练习册系列答案
相关题目