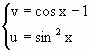题目内容
(1)已知f(2x－1)＝ex，则f(x)＝________．
(2)f(cosx－1)＝sin2x，求f(x)＝________．
(3)f(
)＝
，则f(x)＝________．
答案：
解析：
解析：
|
解答 (1)令2x－1＝t，则x＝ f(t)＝ (2)解法1：令cosx－1＝t，则cosx＝1＋t， 又cosx∈[－1，1]，∴－2≤t≤0 f(t)＝1－(1＋t)2＝－2t－t2(－2≤t≤0) 故f(x)＝－x2－2x(－2≤x≤0) 解法2：参数法令 消去x得u＋(v＋1)2＝1，即u＝－2v－v2 ∴f(x)＝－2x－x2(0≤x≤2) (3)∵f( ＝( ∴f(x)＝x2－x＋1(凑配法) 评析 利用换元法求函数解析式，注意所设元的取值范围． |
，
，∴f(x)＝
)＝
＋1＝
＋1
)2－
＋1
练习册系列答案
相关题目
)＝________．
＋1)＝
，则f(x)＝________．
，则f(x)的解析式为________．