题目内容
已知角a的顶点在原点,始边与x轴的正半轴重合,终边经过点P(-3,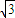 ).
).(1)定义行列式
 =a•d-b•c,解关于x的方程:
=a•d-b•c,解关于x的方程: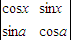 +1=0;
+1=0;(2)若函数f(x)=sin(x+a)+cos(x+a)(x∈R)的图象关于直线x=x对称,求tanx的值.
【答案】分析:(1)由题意先求出角α,有行列式的定义转化为三角函数方程,求x即可.
(2)将f(x)化简为 sin(x+
sin(x+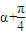 ),由对称轴的特征经过函数的最值点,求出x,再求tanx的值即可.
),由对称轴的特征经过函数的最值点,求出x,再求tanx的值即可.
解答:解:(1)∵角α终边经过点p(3,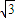 ),∴α=
),∴α= .
.
∴由 可得:cos(x+α)=-1
可得:cos(x+α)=-1
x+α=2k2π+π(k2∈z),∴x=2kπ (k∈z).
(k∈z).
(2)∵f(x)=sin(x+α)+cos(x+α)=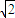 sin(x+
sin(x+ )(x∈R)
)(x∈R)
且函数f(x)的图象关于直线x=x对称,
∴f(x)=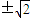 ,即sin(
,即sin( )=±1,
)=±1,
∴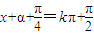 ,
,
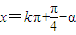 (k∈z).
(k∈z).
tanx=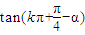 =
=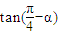 =
=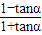 =
= .
.
点评:本题为新定义题,正确理解定义、运用定义转化为熟悉的问题.考查三角函数的化简、求值、及三角函数的性质等问题.
(2)将f(x)化简为
 sin(x+
sin(x+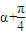 ),由对称轴的特征经过函数的最值点,求出x,再求tanx的值即可.
),由对称轴的特征经过函数的最值点,求出x,再求tanx的值即可.解答:解:(1)∵角α终边经过点p(3,
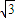 ),∴α=
),∴α= .
.∴由
 可得:cos(x+α)=-1
可得:cos(x+α)=-1x+α=2k2π+π(k2∈z),∴x=2kπ
 (k∈z).
(k∈z).(2)∵f(x)=sin(x+α)+cos(x+α)=
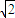 sin(x+
sin(x+ )(x∈R)
)(x∈R)且函数f(x)的图象关于直线x=x对称,
∴f(x)=
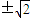 ,即sin(
,即sin( )=±1,
)=±1,∴
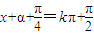 ,
,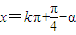 (k∈z).
(k∈z).tanx=
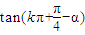 =
=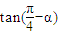 =
=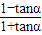 =
= .
.点评:本题为新定义题,正确理解定义、运用定义转化为熟悉的问题.考查三角函数的化简、求值、及三角函数的性质等问题.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 ),且2α∈[0,2π),则tanα等于( )
),且2α∈[0,2π),则tanα等于( )
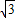
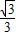

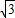 ).
). =a•d-b•c,解关于x的方程:
=a•d-b•c,解关于x的方程: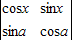 +1=0;
+1=0;