题目内容
下列命题:
①若 与
与 共线,则存在唯一的实数λ,使
共线,则存在唯一的实数λ,使 =λ
=λ ;
;
②空间中,向量 、
、 、
、 共面,则它们所在直线也共面;
共面,则它们所在直线也共面;
③P是△ABC所在平面外一点,O是点P在平面ABC上的射影.若PA、PB、PC两两垂直,则O是△ABC垂心.
④若A,B,C三点不共线,O是平面ABC外一点.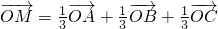 ,则点M一定在平面ABC上,且在△ABC内部.
,则点M一定在平面ABC上,且在△ABC内部.
上述命题中正确的命题是________.
③④
分析:应用平行向量与共线向量,向量的共线定理等知识点,根据向量共线的定义和性质对①②④命题逐一进行判断,对于③,利用线面垂直的判定和性质定理进行证明,即可得到答案.
解答:①中的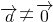 这一条件缺少,于是①错.
这一条件缺少,于是①错.
对于②,因为向量可以任意平移,可知②错;
③当PA,PB,PC两两互相垂直时,则PA⊥平面PBC,则PA⊥BC,
又由PO⊥底面ABC,则PO⊥BC,进而BC⊥平面PAO,即AO⊥BC,
同理可证BO⊥AC,CO⊥AB,故O是△ABC的垂心,即③对;
④中A、B、C、M四点共面.
等式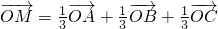 两边同加
两边同加 ,
,
则 (
( +
+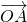 )+
)+ (
( +
+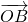 )+
)+ (
( +
+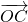 )=
)=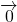 ,
,
即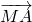 +
+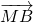 +
+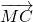 =
=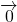 ,
,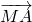 =-(
=-(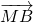 +
+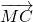 )则
)则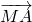 、
、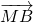 、
、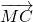 共面,
共面,
又M是三个有向线段的公共点,
则点M一定在平面ABC上,且在△ABC内部.
故④是真命题.
故答案为:③④
点评:本题考查命题的真假判断与应用.在解答向量问题时,向量共线(平行)是最常见的情况之一,我们一定要注意向量平行分为三种情况:①两个非零向量同向;②两个非零向量反向;③零向量与任何一个向量都共线(平行).其中第③种情况,最容易被忽视.
分析:应用平行向量与共线向量,向量的共线定理等知识点,根据向量共线的定义和性质对①②④命题逐一进行判断,对于③,利用线面垂直的判定和性质定理进行证明,即可得到答案.
解答:①中的
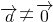 这一条件缺少,于是①错.
这一条件缺少,于是①错.对于②,因为向量可以任意平移,可知②错;
③当PA,PB,PC两两互相垂直时,则PA⊥平面PBC,则PA⊥BC,
又由PO⊥底面ABC,则PO⊥BC,进而BC⊥平面PAO,即AO⊥BC,
同理可证BO⊥AC,CO⊥AB,故O是△ABC的垂心,即③对;
④中A、B、C、M四点共面.
等式
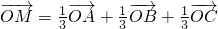 两边同加
两边同加 ,
,则
 (
( +
+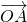 )+
)+ (
( +
+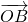 )+
)+ (
( +
+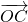 )=
)=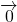 ,
,即
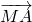 +
+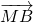 +
+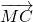 =
=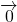 ,
,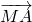 =-(
=-(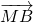 +
+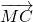 )则
)则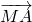 、
、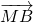 、
、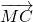 共面,
共面,又M是三个有向线段的公共点,
则点M一定在平面ABC上,且在△ABC内部.
故④是真命题.
故答案为:③④
点评:本题考查命题的真假判断与应用.在解答向量问题时,向量共线(平行)是最常见的情况之一,我们一定要注意向量平行分为三种情况:①两个非零向量同向;②两个非零向量反向;③零向量与任何一个向量都共线(平行).其中第③种情况,最容易被忽视.

练习册系列答案
相关题目
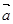 与
与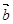 共线,则存在唯一的实数
共线,则存在唯一的实数 ,使
,使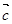 共面,则它们所在直线也共面;
共面,则它们所在直线也共面;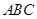 上的射影.若PA 、PB、PC两两垂直,则O是△ABC垂心.
上的射影.若PA 、PB、PC两两垂直,则O是△ABC垂心.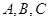 三点不共线,
三点不共线,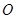 是平面
是平面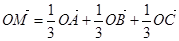 ,则点
,则点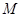 一定在平面
一定在平面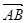 与
与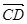 是共线向量,则A、B、C、D四点必在一直线上;
是共线向量,则A、B、C、D四点必在一直线上;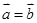 ,
, 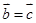 ,则
,则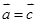 ;
;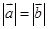 ,则
,则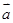 与
与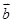 共线,
共线, 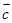 共线,则
共线,则 ·
· =0,则
=0,则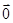 或
或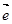 为单位向量且
为单位向量且 共线,则
共线,则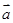 与
与 为非零向量,下列命题:
为非零向量,下列命题: ,
,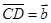 ,
, ;
; ,则
,则 ;
;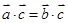 ,
, ,则
,则
 与
与 共线,
共线, 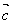 共线,则
共线,则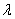 ,使
,使 ,则点M一定在平面ABC上,且在△ABC内部,
,则点M一定在平面ABC上,且在△ABC内部,