题目内容
下列命题:①若 与
与 共线,则存在唯一的实数
共线,则存在唯一的实数 ,使
,使 =
=
 ;
;
②空间中,向量 、
、 、
、 共面,则它们所在直线也共面;
共面,则它们所在直线也共面;
③P是△ABC所在平面外一点,O是点P在平面 上的射影.若PA 、PB、PC两两垂直,则O是△ABC垂心.
上的射影.若PA 、PB、PC两两垂直,则O是△ABC垂心.
④若 三点不共线,
三点不共线, 是平面
是平面 外一点.
外一点. ,则点
,则点 一定在平面
一定在平面 上,且在△ABC内部,上述命题中正确的命题是
.
上,且在△ABC内部,上述命题中正确的命题是
.
【答案】
③④
【解析】本试题主要是考查了平面向量的概念和空间向量的基本定理的运用。
因为
①若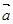 与
与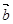 共线,则存在唯一的实数
共线,则存在唯一的实数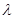 ,使
,使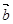 =
=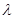
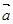 ;当
;当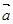 不为零向量时成立。
不为零向量时成立。
②空间中,向量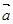 、
、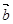 、
、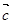 共面,则它们所在直线也共面;也可能一条平行于另外两个向量确定的平面,因此说不成立。
共面,则它们所在直线也共面;也可能一条平行于另外两个向量确定的平面,因此说不成立。
③P是△ABC所在平面外一点,O是点P在平面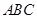 上的射影.若PA 、PB、PC两两垂直,则O是△ABC垂心.成立。
上的射影.若PA 、PB、PC两两垂直,则O是△ABC垂心.成立。
④若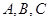 三点不共线,
三点不共线,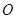 是平面
是平面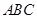 外一点.
外一点.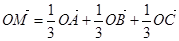 ,则点
,则点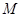 一定在平面
一定在平面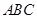 上,且在△ABC内部,成立故正确的命题是③④
上,且在△ABC内部,成立故正确的命题是③④
解决该试题的关键是理解平面向量的共线的运用,和空间向量中共面的判定。

练习册系列答案
相关题目
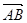 与
与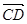 是共线向量,则A、B、C、D四点必在一直线上;
是共线向量,则A、B、C、D四点必在一直线上;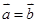 ,
, 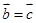 ,则
,则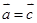 ;
;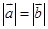 ,则
,则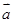 与
与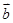 共线,
共线, 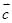 共线,则
共线,则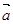 ·
·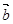 =0,则
=0,则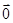 或
或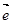 为单位向量且
为单位向量且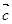 共线,则
共线,则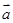 与
与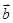 为非零向量,下列命题:
为非零向量,下列命题: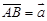 ,
,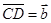 ,
,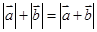 ;
;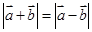 ,则
,则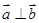 ;
;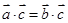 ,
,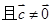 ,则
,则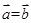
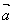 与
与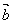 共线,
共线, 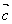 共线,则
共线,则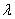 ,使
,使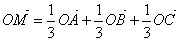 ,则点M一定在平面ABC上,且在△ABC内部,
,则点M一定在平面ABC上,且在△ABC内部,