题目内容
设A={1,2,3,m},B={4,7,n4,n2+3n},m、n∈N,b∈B,“f:a→b=pa+q”是从A到B的一一映射,又1的象是4,7的原象是2,试求p、q、m、n的值.
思路解析:本题是已知一一映射的象和原象,求对应法则,然后再根据对应法则求未知的象与原象.这类问题一般将题意转化为方程或方程组来解.
解:∵1的象是4,∴当a=1时,b=4,
即4=p+q. ①
又∵7的原象是2,
∴当b=7时,a=2,
即7=2p+q. ②
①②联立方程组解,p=3,q=1.
∵“f:a→b=pa+q”是从A到B的一一映射,
∴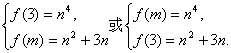
又∵m、n∈N,解得m=5,n=2.

练习册系列答案
相关题目
设a∈{1,2,3,4},b∈{2,4,8,12},则函数f(x)=x3+ax-b在区间[1,2]上有零点的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|