题目内容
已知实数a满足下列两个条件:①关于x的方程ax2+3x+1=0有解;②代数式log2(a+3)有意义.则使得指数函数y=(3a-2)x为减函数的概率为 .
【答案】分析:根据题意先确定是几何概型中的长度类型,由实数a满足下列两个条件得出关于a的不等式,并求出构成的区域长度,再求出指数函数y=(3a-2)x为减函数的数a构成的区域长度,再求两长度的比值.
解答:解::①关于x的方程ax2+3x+1=0有解,
则a=0或△≥0?a≤ ,
,
②代数式log2(a+3)有意义?a>-3.
综合得:-3<a≤ .
.
满足两个条件:①②数a构成的区域长度为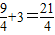 ,
,
指数函数y=(3a-2)x为减函数?0<3a-2<1? <a<1.
<a<1.
则其构成的区域长度为:1- =
= ,
,
则使得指数函数y=(3a-2)x为减函数的概率为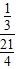 =
=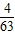 ;
;
故答案为: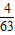 .
.
点评:本题主要考查概率的建模和解模能力,本题是长度类型,思路是先求得试验的全部构成的长度和构成事件的区域长度,再求比值.
解答:解::①关于x的方程ax2+3x+1=0有解,
则a=0或△≥0?a≤
 ,
,②代数式log2(a+3)有意义?a>-3.
综合得:-3<a≤
 .
.满足两个条件:①②数a构成的区域长度为
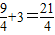 ,
,指数函数y=(3a-2)x为减函数?0<3a-2<1?
 <a<1.
<a<1.则其构成的区域长度为:1-
 =
= ,
,则使得指数函数y=(3a-2)x为减函数的概率为
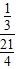 =
=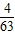 ;
;故答案为:
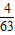 .
.点评:本题主要考查概率的建模和解模能力,本题是长度类型,思路是先求得试验的全部构成的长度和构成事件的区域长度,再求比值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目