函数y=2sin(-2x+ )的单调减区间为A． B． C． D．题目和参考答案——青夏教育精英家教网—

题目内容

函数y=2sin(-2x+ )的单调减区间为（）

A．	B．
C．	D．

解析试题分析：根据题意，由于函数数y=2sin(-2x+)，内层是减函数，则求解复合函数单调减区间，就是求解外层的增区间，整体代入区间中,故解得x的范围是，故选B.
考点：正弦函数的单调性
点评:本题主要考查了正弦函数的单调性．考查了学生对正弦函数基本性质的理解

练习册系列答案

新领程系列答案

相关题目

已知是函数的一条对称轴，且的最大值为，则函数

A．最大值是4，最小值是0	B．最大值是2，最小值是－2
C．最小值不可能是－4	D．最大值可能是0

函数的图像的一条对称轴方程是（）

设函数f(x)=2sin(x+)()与函数的对称轴完全相同，则的值为（）

如图，量角器外缘边上有A，P，Q三点，它们所表示的读数分别是180°，70°，30°，则∠PAQ的大小为【】

为得到函数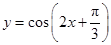的图像，只需将函数的图像( )

A．向右平移个长度单位	B．向左平移个长度单位
C．向左平移个长度单位	D．向右平移个长度单位

将函数的图象向左平移个单位，得到函数的图象．若在[]上为增函数，则的最大值为

函数在一个周期内的图象如下，此函数的解析式为可为( ).

A．	B．
C．	D．

要得到函数的图象，只需将函数的图象（）

A．向右平移个单位	B．向右平移个单位
C．向左平移个单位	D．向左平移个单位

试题分类