题目内容
设实数x1,x2,x3,x4,x5均不小于1,且x1•x2•x3•x4•x5=729,则max{x1x2,x2x3,x3x4,x4x5}的最小值是 .
【答案】分析:先根据基本不等式得x1x2+x3x4≥2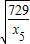 ,即取定一个x5后,x1x2,x3x4不会都小于
,即取定一个x5后,x1x2,x3x4不会都小于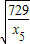 ,及x2x3+x4x5≥2
,及x2x3+x4x5≥2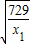
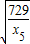 +
+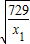 ≥2
≥2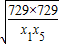 ,再研究使三个不等式等号都成立的条件,即可得出max{x1x2,x2x3,x3x4,x4x5}的最小值.
,再研究使三个不等式等号都成立的条件,即可得出max{x1x2,x2x3,x3x4,x4x5}的最小值.
解答:解:∵x1x2+x3x4≥2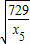 ,即取定一个x5后,x1x2,x3x4不会都小于
,即取定一个x5后,x1x2,x3x4不会都小于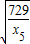 ,
,
同样x2x3+x4x5≥2 ,
,
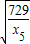 +
+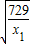 ≥2
≥2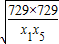 ,
,
使三个不等式等号都成立,则
x1x2=x3x4=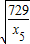 ,
,
x2x3=x4x5=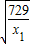 ,
,
x1=x5
即x1=x3=x5,x2=x4 x1x2=x2x3=x3x4=x4x5
所以729=x13×x22=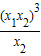 ,(x1x2)3=729×x2
,(x1x2)3=729×x2
x2最小为1,
所以x1x2最小值为9,
此时x1=x3=x5=9 x2=x4=1.
故答案为:9.
点评:本题主要考查了进行简单的合情推理及基本不等式的应用,属于中档题.
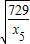 ,即取定一个x5后,x1x2,x3x4不会都小于
,即取定一个x5后,x1x2,x3x4不会都小于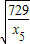 ,及x2x3+x4x5≥2
,及x2x3+x4x5≥2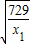
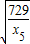 +
+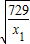 ≥2
≥2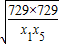 ,再研究使三个不等式等号都成立的条件,即可得出max{x1x2,x2x3,x3x4,x4x5}的最小值.
,再研究使三个不等式等号都成立的条件,即可得出max{x1x2,x2x3,x3x4,x4x5}的最小值.解答:解:∵x1x2+x3x4≥2
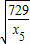 ,即取定一个x5后,x1x2,x3x4不会都小于
,即取定一个x5后,x1x2,x3x4不会都小于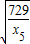 ,
,同样x2x3+x4x5≥2
 ,
,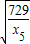 +
+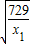 ≥2
≥2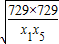 ,
,使三个不等式等号都成立,则
x1x2=x3x4=
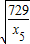 ,
,x2x3=x4x5=
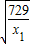 ,
,x1=x5
即x1=x3=x5,x2=x4 x1x2=x2x3=x3x4=x4x5
所以729=x13×x22=
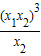 ,(x1x2)3=729×x2
,(x1x2)3=729×x2 x2最小为1,
所以x1x2最小值为9,
此时x1=x3=x5=9 x2=x4=1.
故答案为:9.
点评:本题主要考查了进行简单的合情推理及基本不等式的应用,属于中档题.

练习册系列答案
相关题目