题目内容
已知- <x<0,sinx+cosx=
<x<0,sinx+cosx= .
.
(1)求sinx-cosx的值;
(2)求 的值.
的值.
 <x<0,sinx+cosx=
<x<0,sinx+cosx= .
.(1)求sinx-cosx的值;
(2)求
 的值.
的值.(1)sinx-cosx=- (2)
(2)
 (2)
(2)
(1)方法一 联立方程:

 2分
2分
由①得sinx= -cosx,将其代入②,整理得
-cosx,将其代入②,整理得
25cos2x-5cosx-12="0. " 4分
∵- <x<0,
<x<0,
∴ ,
,
所以sinx-cosx=- . 7分
. 7分
方法二 ∵sinx+cosx= ,
,
∴(sinx+cosx)2= ,
,
即1+2sinxcosx= ,
,
∴2sinxcosx=- . 2分
. 2分
∵(sinx-cosx)2=sin2x-2sinxcosx+cos2x
=1-2sinxcosx=1+ =
= ① 4分
① 4分
又∵- <x<0,∴sinx<0,cosx>0,
<x<0,∴sinx<0,cosx>0,
∴sinx-cosx<0 ②
由①②可知:sinx-cosx=- . 7分
. 7分
(2)由已知条件及(1)可知
 ,解得
,解得 , 9分
, 9分
∴tanx=- . 11分
. 11分
又∵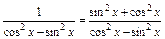
=
= 13分
13分
= . 14分
. 14分

 2分
2分由①得sinx=
 -cosx,将其代入②,整理得
-cosx,将其代入②,整理得25cos2x-5cosx-12="0. " 4分
∵-
 <x<0,
<x<0,∴
 ,
,所以sinx-cosx=-
 . 7分
. 7分方法二 ∵sinx+cosx=
 ,
,∴(sinx+cosx)2=
 ,
,即1+2sinxcosx=
 ,
,∴2sinxcosx=-
 . 2分
. 2分∵(sinx-cosx)2=sin2x-2sinxcosx+cos2x
=1-2sinxcosx=1+
 =
= ① 4分
① 4分又∵-
 <x<0,∴sinx<0,cosx>0,
<x<0,∴sinx<0,cosx>0,∴sinx-cosx<0 ②
由①②可知:sinx-cosx=-
 . 7分
. 7分(2)由已知条件及(1)可知
 ,解得
,解得 , 9分
, 9分∴tanx=-
 . 11分
. 11分又∵
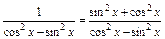
=

=
 13分
13分=
 . 14分
. 14分
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 ,2kπ+π)(k∈Z),求角α的各三角函数值.
,2kπ+π)(k∈Z),求角α的各三角函数值. 求:cosα和tanα的值.
求:cosα和tanα的值. ,求(1)
,求(1) ;
; 的值.
的值. ,那么
,那么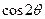 的值等于________.
的值等于________.
 ,则
,则 的值为( )
的值为( )



 ,则
,则 的值为( )
的值为( )



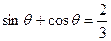 ,则
,则 值为( )
值为( ) ,则
,则 .
.