题目内容
(2007
北京崇文模拟)如果函数f(x)在区间D上有定义,且对任意 都有
都有 ,则称函数f(x)是区间D上的“凹函数”.
,则称函数f(x)是区间D上的“凹函数”.
(1)
已知 ,决断f(x)是否是“凹函数”,若是,请给出证明;若不是,请说明理由;
,决断f(x)是否是“凹函数”,若是,请给出证明;若不是,请说明理由;
(2)
对于(1)中的函数f(x)有下列性质:“若 [a,b],则存在
[a,b],则存在 使得
使得 ”成立.利用这个性质证明
”成立.利用这个性质证明 唯一;
唯一;
(3)
设A、B、C是函数 图象上三个不同的点,求证:△ABC是钝角三角形.
图象上三个不同的点,求证:△ABC是钝角三角形.
答案:略
解析:
解析:
|
解析: (1)函数f(x)是凹函数,证明如下:设 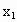 , , ,且 ,且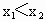 ,则 ,则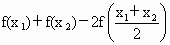
∵
∴ ∴ ∴ ∴ ∴ 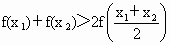 ,∴ ,∴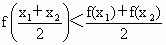 , ,
∴ f(x)是凹函数.(2) 假设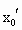 , ,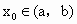 ,且 ,且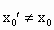 ,使得 ,使得
①-②得 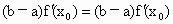 , ,
∵ b>a,∴b-a≠0.∴ 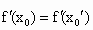 , ,
∵ 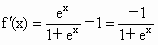 , ,
记 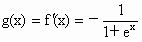 , ,
∴ 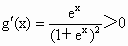 . .
∴ 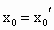 ,这与 ,这与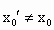 矛盾,即 矛盾,即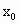 是唯一的. 是唯一的.
(3) 设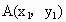 , , , ,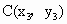 ,且 ,且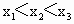 ,∵ ,∵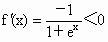 , ,
∴ f(x)是x R上的单调减函数. R上的单调减函数.
∴ 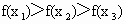 . .
∵ 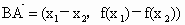 , ,
∴ 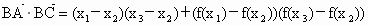 . .
∵ 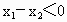 , ,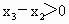 , ,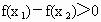 , ,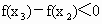 , ,
∴ 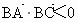 ,∴cosB<0,∠B为钝角. ,∴cosB<0,∠B为钝角.
故△ ABC为钝角三角形. |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
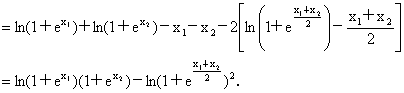
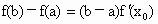
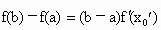
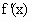
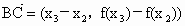
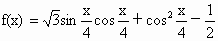 .
.
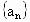 中,对任意
中,对任意 ,都有
,都有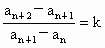 (k为常数),则称
(k为常数),则称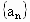 为“等差比数列”,下面对“等差比数列”的判断:①k不可能为0;②等差数列一定是等差比数列;③等比数列一定是等差比数列;④通项公式为
为“等差比数列”,下面对“等差比数列”的判断:①k不可能为0;②等差数列一定是等差比数列;③等比数列一定是等差比数列;④通项公式为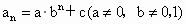 的数列一定是等差比数列,其中正确的判断
的数列一定是等差比数列,其中正确的判断
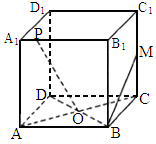
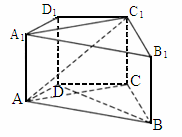
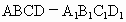 中,M是
中,M是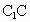 的中点,O是底面ABCD的中心,P是
的中点,O是底面ABCD的中心,P是 上的任意点,则直线BM与OP所成的角为__________°.
上的任意点,则直线BM与OP所成的角为__________°.
 中,∠ADC=90°,△ABC为等边三角形,且
中,∠ADC=90°,△ABC为等边三角形,且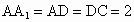 .
.
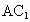 与BC所成角的余弦值;
与BC所成角的余弦值;
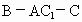 的大小;
的大小;
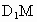 ⊥平面
⊥平面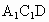 ?并证明你的结论.
?并证明你的结论.
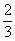 和
和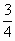 ,假设两人每次射击是否击中目标相互之间没有影响.
,假设两人每次射击是否击中目标相互之间没有影响.