题目内容
已知关于x的二项式 展开式的二项式系数之和为32,常数项为80,则a的值为( )
展开式的二项式系数之和为32,常数项为80,则a的值为( )A.1
B.±1
C.2
D.±2
【答案】分析:根据题意,有2n=32,可得n=5,进而可得其展开式为Tr+1=C5r•( )5-r•(
)5-r•(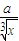 )r,分析可得其常数项为第4项,即C53•(a)3,
)r,分析可得其常数项为第4项,即C53•(a)3,
依题意,可得C53•(a)3=80,解可得a的值.
解答:解:根据题意,该二项式的展开式的二项式系数之和为32,则有2n=32,
可得n=5,
则二项式的展开式为Tr+1=C5r•(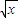 )5-r•(
)5-r•(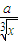 )r,
)r,
其常数项为第4项,即C53•(a)3,
根据题意,有C53•(a)3=80,
解可得,a=2;
故选C.
点评:本题考查二项式定理的应用,注意二项式的展开式的形式,要求准确记忆.
 )5-r•(
)5-r•(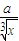 )r,分析可得其常数项为第4项,即C53•(a)3,
)r,分析可得其常数项为第4项,即C53•(a)3,依题意,可得C53•(a)3=80,解可得a的值.
解答:解:根据题意,该二项式的展开式的二项式系数之和为32,则有2n=32,
可得n=5,
则二项式的展开式为Tr+1=C5r•(
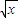 )5-r•(
)5-r•(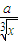 )r,
)r,其常数项为第4项,即C53•(a)3,
根据题意,有C53•(a)3=80,
解可得,a=2;
故选C.
点评:本题考查二项式定理的应用,注意二项式的展开式的形式,要求准确记忆.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 展开式的二项式系数之和为32,常数项为80,则a的值为( )
展开式的二项式系数之和为32,常数项为80,则a的值为( ) C.2
D.
C.2
D.
 展开式的二项式系数之和为32,常数项为80,则a的值为 ( )
展开式的二项式系数之和为32,常数项为80,则a的值为 ( ) C.2 D.
C.2 D.
 展开式的二项式系数之和为32,常数项为80,则a的值为( )
展开式的二项式系数之和为32,常数项为80,则a的值为( ) C.2 D.
C.2 D.
 展开式的二项式系数之和为32,常数项为80,则a的值为(
)
展开式的二项式系数之和为32,常数项为80,则a的值为(
) C.1 D.
C.1 D.