题目内容
分别以双曲线G:
-
=1的焦点为顶点,以双曲线G的顶点为焦点作椭圆C.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设点P的坐标为(0,3),在y轴上是否存在定点M,过点M且斜率为k的动直线l 交椭圆于A、B两点,使以AB为直径的圆恒过点P,若存在,求出M的坐标;若不存在,说明理由.
| x2 |
| 16 |
| y2 |
| 9 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)设点P的坐标为(0,3),在y轴上是否存在定点M,过点M且斜率为k的动直线l 交椭圆于A、B两点,使以AB为直径的圆恒过点P,若存在,求出M的坐标;若不存在,说明理由.
分析:(Ⅰ)确定双曲线G:
-
=1的焦点为(±5,0),顶点为(±4,0),从而可得椭圆的顶点与焦点,进而可求椭圆方程;
(Ⅱ)假设存在M(0,a),过点M且斜率为k的动直线l交椭圆于A、B两点,使以AB为直径的圆恒过点P,AB方程为y=kx+a,代入方程C:
+
=1,消去y,得(9+25k2)x2+50akx+25a2-225=0,利用韦达定理结合
•
=0,即可知M点的坐标存在.
| x2 |
| 16 |
| y2 |
| 9 |
(Ⅱ)假设存在M(0,a),过点M且斜率为k的动直线l交椭圆于A、B两点,使以AB为直径的圆恒过点P,AB方程为y=kx+a,代入方程C:
| x2 |
| 25 |
| y2 |
| 9 |
| PA |
| PB |
解答:解:(Ⅰ)双曲线G:
-
=1的焦点为(±5,0),顶点为(±4,0),
所以所求椭圆方程为C:
+
=1…(5分)
(Ⅱ)假设存在M(0,a),过点M且斜率为k的动直线l交椭圆于A、B两点,使以AB为直径的圆恒过点P,
AB方程为y=kx+a,代入方程C:
+
=1,
消去y,得(9+25k2)x2+50akx+25a2-225=0,…(7分)
设A(x1,y1),B(x2,y2)则x1+x2=
,x1x2=
…(9分)
•
=(x1,y1-3)•(x2,y2-3)=x1x2+y1y2-3(y1+y2)+9
=x1x2+(kx1+a)(kx2+a)-3k(x1+x2)-6a+9=(k2+1)x1x2+k(a-3)( x1+x2)+a2-6a+9
=(k2+1)
+k(a-3)
+a2-6a+9
由以AB为直径的圆恒过点P,可得
•
=0,得17a2-27a-72=0,
∴(17a+24)(a-3)=0…(12分)
∴a=3,或a=-
∵点P的坐标为(0,3),过点M且斜率为k的动直线l 交椭圆于A、B两点
∴a=-
故M点的坐标存在,M的坐标为(0,-
)…(13分)
| x2 |
| 16 |
| y2 |
| 9 |
所以所求椭圆方程为C:
| x2 |
| 25 |
| y2 |
| 9 |
(Ⅱ)假设存在M(0,a),过点M且斜率为k的动直线l交椭圆于A、B两点,使以AB为直径的圆恒过点P,
AB方程为y=kx+a,代入方程C:
| x2 |
| 25 |
| y2 |
| 9 |
消去y,得(9+25k2)x2+50akx+25a2-225=0,…(7分)
设A(x1,y1),B(x2,y2)则x1+x2=
| -50ak |
| 9+25k2 |
| 25a2-225 |
| 9+25k2 |
| PA |
| PB |
=x1x2+(kx1+a)(kx2+a)-3k(x1+x2)-6a+9=(k2+1)x1x2+k(a-3)( x1+x2)+a2-6a+9
=(k2+1)
| 25a2-225 |
| 9+25k2 |
| -50ak |
| 9+25k2 |
由以AB为直径的圆恒过点P,可得
| PA |
| PB |
∴(17a+24)(a-3)=0…(12分)
∴a=3,或a=-
| 24 |
| 17 |
∵点P的坐标为(0,3),过点M且斜率为k的动直线l 交椭圆于A、B两点
∴a=-
| 24 |
| 17 |
故M点的坐标存在,M的坐标为(0,-
| 24 |
| 17 |
点评:本题考查双曲线、椭圆的几何性质,考查椭圆的标准方程,考查直线与椭圆的位置关系,考查恒成立问题的处理,解题要细心.

练习册系列答案
相关题目
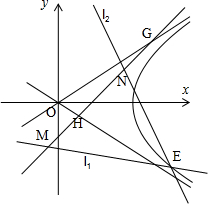
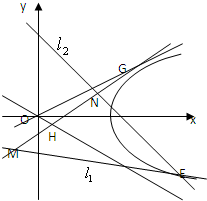
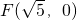 为右焦点的双曲线C的离心率
为右焦点的双曲线C的离心率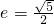 .
.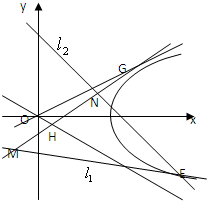 .
. ,0)为右焦点的双曲线C的离心率
,0)为右焦点的双曲线C的离心率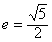 。
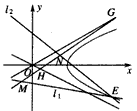
。
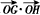 的值。
的值。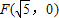 为右焦点的双曲线C的离心率
为右焦点的双曲线C的离心率 .
.
 为右焦点的双曲线C的离心率
为右焦点的双曲线C的离心率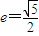 .
.