题目内容
设m个不全相等的正数a1,a2,…,am(m≥7)依次围成一个圆圈,(Ⅰ)若m=2009,且a1,a2,…,a1005是公差为d的等差数列,而a1,a2009,a2008,…,a1006是公比为q=d的等比数列;数列a1,a2,…,am的前n项和Sn(n≤m)满足:S3=15,S2009=S2007+12a1,求通项an(n≤m);
(Ⅱ)若每个数an(n≤m)是其左右相邻两数平方的等比中项,求证:a1+…+a6+a72+…+am2>ma1a2am.
【答案】分析:(1)利用等比数列的性质,用a1、d表示出a2009、a2008,结合已知,列方程即可解出a1、d,进而求出an.
(2)通过探求数列的周期性或利用反证法求解.
解答:解:(I)因a1,a2009,a2008,a1006是公比为d的等比数列,
从而a2009=a1d,a2008=a1d2,
由S2009=S2007+12a1得a2008+a2009=12a1,
解得d=3或d=-4(舍去).
∴d=3,
又S3=3a1+3d=15.解得a1=2
从而当n≤1005时,an=a1+(n-1)d=2+3(n-1)=3n-1
当1006≤n≤2009时,由a1,a2009,a2008,a1006是公比为d的等比数列
得an=a1d2009-(n-1)=a1d2010-n(1006≤n≤2009)
因此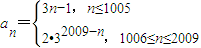
(II)由题意an2=an-12an+12(1<n<m),am2=am-12a12,a12=am2a22
得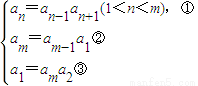
有①得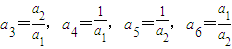 ④
④
由①,②,③得a1a2an=(a1a2an)2,
故a1a2an=1.⑤
又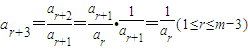 ,
,
故有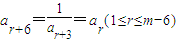 .⑥
.⑥
下面反证法证明:m=6k
若不然,设m=6k+p,其中1≤p≤5
若取p=1即m=6k+1,则由⑥得am=a6k+1=a1,
而由③得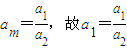 ,
,
得a2=1,由②得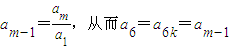 ,
,
而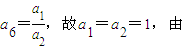 ④及⑥可推得an=1(1≤n≤m)与题设矛盾
④及⑥可推得an=1(1≤n≤m)与题设矛盾
同理若P=2,3,4,5均可得an=1(1≤n≤m)与题设矛盾,
因此m=6k为6的倍数
由均值不等式得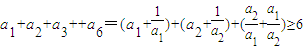
由上面三组数内必有一组不相等(否则a1=a2=a3=1,
从而a4=a5═am=1与题设矛盾),故等号不成立,
从而a1+a2+a3++a6>6又m=6k,由④和⑥得
a72++am2=(a72++a122)++(a6k-52++a6k2)
=(k-1)(a12++a62)
=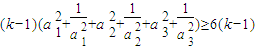
因此由⑤得a1+a2+a3++a6+a72++am2>6+6(k-1)=6k=m=ma1a2a3am
点评:本题考查了等差数列和等比数列的通项公式、性质及方程、解不等式的有关知识,考查运算能力和推理能力.
(2)通过探求数列的周期性或利用反证法求解.
解答:解:(I)因a1,a2009,a2008,a1006是公比为d的等比数列,
从而a2009=a1d,a2008=a1d2,
由S2009=S2007+12a1得a2008+a2009=12a1,
解得d=3或d=-4(舍去).
∴d=3,
又S3=3a1+3d=15.解得a1=2
从而当n≤1005时,an=a1+(n-1)d=2+3(n-1)=3n-1
当1006≤n≤2009时,由a1,a2009,a2008,a1006是公比为d的等比数列
得an=a1d2009-(n-1)=a1d2010-n(1006≤n≤2009)
因此
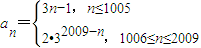
(II)由题意an2=an-12an+12(1<n<m),am2=am-12a12,a12=am2a22
得
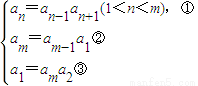
有①得
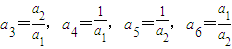 ④
④由①,②,③得a1a2an=(a1a2an)2,
故a1a2an=1.⑤
又
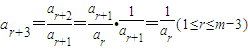 ,
,故有
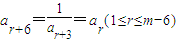 .⑥
.⑥下面反证法证明:m=6k
若不然,设m=6k+p,其中1≤p≤5
若取p=1即m=6k+1,则由⑥得am=a6k+1=a1,
而由③得
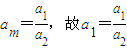 ,
,得a2=1,由②得
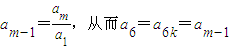 ,
,而
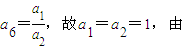 ④及⑥可推得an=1(1≤n≤m)与题设矛盾
④及⑥可推得an=1(1≤n≤m)与题设矛盾同理若P=2,3,4,5均可得an=1(1≤n≤m)与题设矛盾,
因此m=6k为6的倍数
由均值不等式得
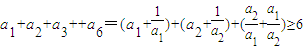
由上面三组数内必有一组不相等(否则a1=a2=a3=1,
从而a4=a5═am=1与题设矛盾),故等号不成立,
从而a1+a2+a3++a6>6又m=6k,由④和⑥得
a72++am2=(a72++a122)++(a6k-52++a6k2)
=(k-1)(a12++a62)
=
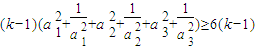
因此由⑤得a1+a2+a3++a6+a72++am2>6+6(k-1)=6k=m=ma1a2a3am
点评:本题考查了等差数列和等比数列的通项公式、性质及方程、解不等式的有关知识,考查运算能力和推理能力.

练习册系列答案
相关题目
 。
。