题目内容
在以下4个命题中:①a+b+| 1 | ||
|
| 2 |
分析:对于①②,利用不等式的性质及特值法相结合进行判断;对于③④利用直线方程的表示形式进行判断.
解答:解:①取a=-1,b=-1,左边=-1,不等式显然不成立.①错误
②若实数ab满足ab<0,则应有|a-b|=|a|+|b|;②错误
③经过定点A(0,b),且与x轴垂直的直线,斜率不存在,不能用方程y=kx+b表示.③错误
④在坐标平面内,二元一次不等式表示直线一侧的区域,∴对于在直线Ax+By+C=0同一侧所有点(x,y),实数Ax+By+C的符号相同 ④正确
故答案为:①②③
②若实数ab满足ab<0,则应有|a-b|=|a|+|b|;②错误
③经过定点A(0,b),且与x轴垂直的直线,斜率不存在,不能用方程y=kx+b表示.③错误
④在坐标平面内,二元一次不等式表示直线一侧的区域,∴对于在直线Ax+By+C=0同一侧所有点(x,y),实数Ax+By+C的符号相同 ④正确
故答案为:①②③
点评:本题考查不等式的基本性质,要注意基本不等式成立的条件是a,b均为正数.还考查直线方程的表示形式,及二元一次不等式得解集与平面区域的对应关系.

练习册系列答案
相关题目
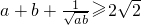 ; ②若实数ab满足ab<0,则有|a-b|<|a|+|b|; ③经过定点A(0,b)的直线都可以用方程y=kx+b表示; ④对于在直线Ax+By+C=0同一侧所有点(x,y),实数Ax+By+C的符号相同.错误命题的序号是________.(把你认为错误的命题的序号都填上)
; ②若实数ab满足ab<0,则有|a-b|<|a|+|b|; ③经过定点A(0,b)的直线都可以用方程y=kx+b表示; ④对于在直线Ax+By+C=0同一侧所有点(x,y),实数Ax+By+C的符号相同.错误命题的序号是________.(把你认为错误的命题的序号都填上)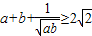 ; ②若实数ab满足ab<0,则有|a-b|<|a|+|b|; ③经过定点A(0,b)的直线都可以用方程y=kx+b表示; ④对于在直线Ax+By+C=0同一侧所有点(x,y),实数Ax+By+C的符号相同.错误命题的序号是 .(把你认为错误的命题的序号都填上)
; ②若实数ab满足ab<0,则有|a-b|<|a|+|b|; ③经过定点A(0,b)的直线都可以用方程y=kx+b表示; ④对于在直线Ax+By+C=0同一侧所有点(x,y),实数Ax+By+C的符号相同.错误命题的序号是 .(把你认为错误的命题的序号都填上)