题目内容
(12分)已知函数![]()
(Ⅰ)若函数![]() 在
在![]() 上为增函数,求正实数
上为增函数,求正实数![]() 的取值范围;
的取值范围;
解析:(Ⅰ)由已知得![]() ………………2分
………………2分
依题意:![]() 对
对![]() 恒成立………………3分
恒成立………………3分
即:![]() 对
对![]() 恒成立
恒成立
也即:![]() 对
对![]() 恒成立
恒成立
∴![]() 即
即![]() ………………5分
………………5分
(Ⅱ)∵![]()
∴![]() 在定义域
在定义域![]() 上满足
上满足![]() 在
在![]() 上是减函数,
上是减函数,
在![]() 是增函数………………6分
是增函数………………6分
![]() 当
当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上是增函数………………8分
上是增函数………………8分
![]() 当
当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上是减函数……………10分
上是减函数……………10分
![]() 当
当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上是减函数,
上是减函数,![]() 在
在![]() 上是增函数………………12分
上是增函数………………12分

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
已知函数 ,(
,( ),
),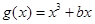
(1)若曲线 与曲线
与曲线 在它们的交点(1,c)处具有公共切线,求a,b的值
在它们的交点(1,c)处具有公共切线,求a,b的值
(2)当 时,若函数
时,若函数 的单调区间,并求其在区间(-∞,-1)上的最大值。
的单调区间,并求其在区间(-∞,-1)上的最大值。
【解析】(1) ,
,
∵曲线 与曲线
与曲线 在它们的交点(1,c)处具有公共切线
在它们的交点(1,c)处具有公共切线
∴ ,
,
∴
(2)令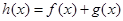 ,当
,当 时,
时,
 令
令 ,得
,得
 时,
时,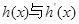 的情况如下:
的情况如下:
|
x |
|
|
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
|
|
|
|
所以函数 的单调递增区间为
的单调递增区间为 ,
, ,单调递减区间为
,单调递减区间为
当 ,即
,即 时,函数
时,函数 在区间
在区间 上单调递增,
上单调递增, 在区间
在区间 上的最大值为
上的最大值为 ,
,
当 且
且 ,即
,即 时,函数
时,函数 在区间
在区间 内单调递增,在区间
内单调递增,在区间 上单调递减,
上单调递减, 在区间
在区间 上的最大值为
上的最大值为
当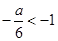 ,即a>6时,函数
,即a>6时,函数 在区间
在区间 内单调递赠,在区间
内单调递赠,在区间 内单调递减,在区间
内单调递减,在区间 上单调递增。又因为
上单调递增。又因为
所以 在区间
在区间 上的最大值为
上的最大值为 。
。
 +bx) (a>0且a≠1),则下列叙述正确的是( )
+bx) (a>0且a≠1),则下列叙述正确的是( ) ,b=-1,则函数f(x)为R上的增函数
,b=-1,则函数f(x)为R上的增函数 ,b=-1,则函数f(x)为R上的减函数
,b=-1,则函数f(x)为R上的减函数



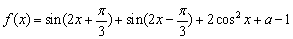 (
( 为常数),若函数
为常数),若函数 的最大值为
的最大值为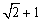 .
. 的图象向左平移
的图象向左平移 个单位,再向下平移2个单位得到函数
个单位,再向下平移2个单位得到函数 的图象,求函数
的图象,求函数 的单调递减区间.
的单调递减区间.