题目内容
已知数列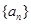 的前
的前 项和
项和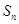 和通项
和通项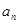 满足
满足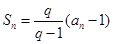 (
(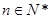 ,
,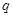 是大于0的常数,且
是大于0的常数,且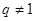 ),数列
),数列 是公比不为
是公比不为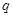 的等比数列,
的等比数列,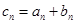 .
.
(1)求数列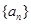 的通项公式;
的通项公式;
(2)设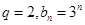 ,是否存在实数
,是否存在实数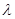 ,使数列
,使数列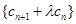 是等比数列?若存在,求出所有可能的实数
是等比数列?若存在,求出所有可能的实数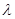 的值,若不存在说明理由;
的值,若不存在说明理由;
(3)数列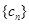 是否能为等比数列?若能,请给出一个符合的条件的
是否能为等比数列?若能,请给出一个符合的条件的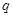 和
和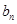 的组合,若不能,请说明理由.
的组合,若不能,请说明理由.
(1)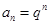 ,(2)λ= 2或λ= 3,(3)不可能为等比数列.
,(2)λ= 2或λ= 3,(3)不可能为等比数列.
解析试题分析:(1)求一般数列通项,常利用和项与通项关系,即当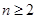 时,
时,  ,整理得
,整理得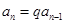 ,又由
,又由 ,得
,得 ,
,
结合q>0知,数列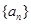 是首项为q公比为
是首项为q公比为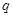 的等比数列, ∴
的等比数列, ∴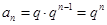 (2)存在性问题,一般从假设存在出发,探求等量关系,将是否存在转化为是否有解. 结合(1)知,当q=2时,
(2)存在性问题,一般从假设存在出发,探求等量关系,将是否存在转化为是否有解. 结合(1)知,当q=2时,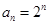 ,所以
,所以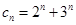 ,假设存在实数
,假设存在实数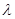 ,使数列
,使数列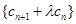 是等比数列,则对任意n≥2有(cn+1+λcn)2=(cn+2+λcn+1)(cn+λcn 1),将cn=2n+3n代入上式,整理得
是等比数列,则对任意n≥2有(cn+1+λcn)2=(cn+2+λcn+1)(cn+λcn 1),将cn=2n+3n代入上式,整理得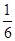 (2+λ)(3+λ)·2n·3n=0,解得λ= 2或λ= 3.(3)首先利用特殊值探讨,得出结论是数列
(2+λ)(3+λ)·2n·3n=0,解得λ= 2或λ= 3.(3)首先利用特殊值探讨,得出结论是数列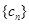 不可能为等比数列.说明也可根据特例. 由题意得c1c3 c22=b1q(p2+q2 2pq),由于p≠q时,p2+q2>2pq,又q及等比数列的首项b1均不为零,所以 c1c3 c22≠0,即 c22≠c1·c3. 故{cn}不是等比数列.
不可能为等比数列.说明也可根据特例. 由题意得c1c3 c22=b1q(p2+q2 2pq),由于p≠q时,p2+q2>2pq,又q及等比数列的首项b1均不为零,所以 c1c3 c22≠0,即 c22≠c1·c3. 故{cn}不是等比数列.
解:(1)当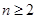 时,
时,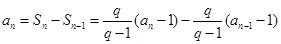 ,整理得
,整理得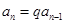 2分
2分
又由 ,得
,得 3分
3分
结合q>0知,数列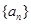 是首项为q公比为
是首项为q公比为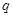 的等比数列, ∴
的等比数列, ∴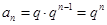 5分
5分
(2)结合(1)知,当q=2时,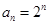 ,所以
,所以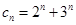 6分
6分
假设存在实数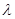 ,使数列
,使数列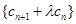 是等比数列,则对任意n≥2有
是等比数列,则对任意n≥2有
(cn+1+λcn)2=(cn+2+λcn+1)(cn+λcn 1),将cn=2n+3n代入上式,得:
[2n+1+3n+1+λ(2n+3n)]2=[2n+2+3n+2+λ(2n+1+3n+1)]·[2n+3n+λ(2n 1+3n 1)],
即 [(2+λ)2n+(3+λ)3n]2=[(2+λ)2n+1+(3+λ)3n+1][(2+λ)2n 1+(3+λ)3n 1],
整理得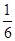 (2+λ)(3+λ)·2n·3n=0,解得λ= 2或λ= 3. 10分
(2+λ)(3+λ)·2n·3n=0,解得λ= 2或λ= 3. 10分
故存在实数实数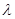 = 2或 3,使数列
= 2或 3,使数列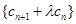 是等比数列. 11分
是等比数列. 11分
(3)数列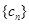 不可能为等比数列. 12分
不可能为等比数列. 12分
理由如下:
设等比数列{bn}的公比为p,则由题设知p≠q,则cn=qn+b1pn 1
为要证{cn}不是等比数列只需证c22≠c1·c3.
事实上,
c22=(q2+b1p)2=q4+2q2b1p+b12p2, ①
c1·c3=(q+b1)(q3+b1p2)=q4+b12p2+b1q(p2+q2), ②
②-①得
c1c3 c22=b1q(p2+q2 2pq)
由于p≠q时,p2+q2>2pq,又q及等比数列的首项b1均不为零,
所以 c1c3 c22≠0,即 c22≠c1·c3. 故{cn}不是等比数列. 16分
考点:数列和项与通项关系,数列综合应用

设等差数列 的前n项和为
的前n项和为 ,若
,若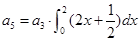 ,则
,则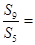 ( ).
( ).
| A.9 | B.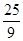 | C.2 | D.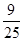 |
 满足
满足 ,
,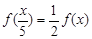 ,且当
,且当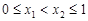 时,
时, ,则
,则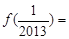 .
.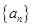 中,
中,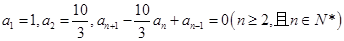
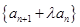 是等比数列, 求实数
是等比数列, 求实数 ;
;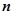 项和
项和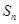 .
.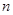 等分(
等分(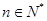 且
且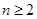 ),在相重叠的扇形格中依次同时填上
),在相重叠的扇形格中依次同时填上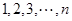 ,内圆盘可绕圆心旋转,每次可旋转一个扇形格,当内圆盘旋转到某一位置时,定义所有重叠扇形格中两数之积的和为此位置的“旋转和”.
,内圆盘可绕圆心旋转,每次可旋转一个扇形格,当内圆盘旋转到某一位置时,定义所有重叠扇形格中两数之积的和为此位置的“旋转和”.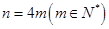 ,在如图所示的初始位置将任意
,在如图所示的初始位置将任意 对重叠的扇形格中的两数均改写为0,证明:当
对重叠的扇形格中的两数均改写为0,证明:当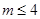 时,通过旋转,总存在一个位置,任意重叠的扇形格中两数不同时为0.
时,通过旋转,总存在一个位置,任意重叠的扇形格中两数不同时为0.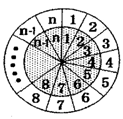
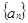 的前
的前 项和
项和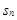 满足
满足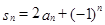 ,
,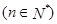
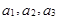
 ,求证:数列
,求证:数列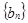 为等比数列,并指出
为等比数列,并指出 的各项都是正数,且对任意
的各项都是正数,且对任意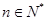 都有
都有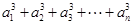
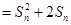 ,其中
,其中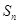 为数列
为数列 项和.
项和. 、
、 ;
;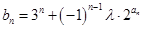 ,对任意的
,对任意的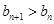 恒成立,求实数
恒成立,求实数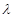 的取值范围.
的取值范围.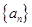 满足
满足 ,
, 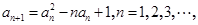
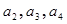 ;
;
 与所搭三角形的个数
与所搭三角形的个数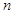 之间的关系式可以是
之间的关系式可以是