题目内容
在2008年北京奥运会垒球比赛前,中国教练布置战术时,要求击球手与连接本垒游击手的直线成15°的方向把球击出.根据经验及测速仪的显示,通常情况下球速为游击手最大跑速的4倍.问按这样的布置,游击手能不能接着球?分析:先假设能够接到球且接球点为B,设游击手从点A跑出,本垒为O点构造三角形OAB,再假设从击出球到接着球的时间为t,球速为v,在三角形POAB中可得到OB=vt,AB≤
•t,然后根据正弦定理可得到sin∠OAB的值,结果发现sin∠OAB>1不成立,故接不到球.
| v |
| 4 |
解答: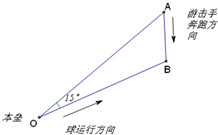 解:如图,设游击手能接着球,接球点为B,而游击手从点A跑出,本垒为O点.
解:如图,设游击手能接着球,接球点为B,而游击手从点A跑出,本垒为O点.
设从击出球到接着球的时间为t,球速为v,则∠AOB=15°,
OB=vt,AB≤
•t.
在△AOB中,由正弦定理,得
=
,
sin∠OAB=
≥
=
-
,
而(
-
)2=8-4
>8-4×1.74>1,
即sin∠OAB>1,
∴这样的∠OAB不存在,因此游击手不能接着球.
 解:如图,设游击手能接着球,接球点为B,而游击手从点A跑出,本垒为O点.
解:如图,设游击手能接着球,接球点为B,而游击手从点A跑出,本垒为O点.设从击出球到接着球的时间为t,球速为v,则∠AOB=15°,
OB=vt,AB≤
| v |
| 4 |
在△AOB中,由正弦定理,得
| OB |
| sin∠OAB |
| AB |
| sin 15° |
sin∠OAB=
| OBsin 15° |
| AB |
| ||||
| 4 |
| 6 |
| 2 |
而(
| 6 |
| 2 |
| 3 |
即sin∠OAB>1,
∴这样的∠OAB不存在,因此游击手不能接着球.
点评:本题主要考查正弦定理在现实生活中的应用.考查考生的对问题的理解和认识的深度.

练习册系列答案
相关题目
 在2008年北京奥运会青岛奥帆赛举行之前,为确保赛事安全,青岛海事部门举行奥运安保海上安全演习.为了测量正在海面匀速行驶的某航船的速度,在海岸上选取距离为1千米的两个观察点C,D,在某天10:00观察到该航船在A处,此时测得∠ADC=30°,3分钟后该船行驶至B处,此时测得∠ACB=60°,∠BCD=45°,∠ADB=60°,则船速为
在2008年北京奥运会青岛奥帆赛举行之前,为确保赛事安全,青岛海事部门举行奥运安保海上安全演习.为了测量正在海面匀速行驶的某航船的速度,在海岸上选取距离为1千米的两个观察点C,D,在某天10:00观察到该航船在A处,此时测得∠ADC=30°,3分钟后该船行驶至B处,此时测得∠ACB=60°,∠BCD=45°,∠ADB=60°,则船速为 在2008年北京奥运会上,林跃.火亮为观众上演了一场精彩的表演,最终以468.18的高分毫无悬念的夺得男子10米比双人跳台的冠军,这次比赛共有7名裁判打分,在第二轮跳水中,林跃.火亮的难度系数为2.0,7名评委给他们评定的成绩分别是:10,9.5,10,10,9.5,10,10,程序框图用来编写程序统计每位选手的成绩,试根据下面所给条件回答下列问题:
在2008年北京奥运会上,林跃.火亮为观众上演了一场精彩的表演,最终以468.18的高分毫无悬念的夺得男子10米比双人跳台的冠军,这次比赛共有7名裁判打分,在第二轮跳水中,林跃.火亮的难度系数为2.0,7名评委给他们评定的成绩分别是:10,9.5,10,10,9.5,10,10,程序框图用来编写程序统计每位选手的成绩,试根据下面所给条件回答下列问题: