题目内容
2.已知平面上的点集A及点P,在集合A内任取一点Q,线段PQ长度的最小值称为点P到集合A的距离,记作d(P,A).如果集合A={(x,y)|x+y=1(0≤x≤1)},点P的坐标为(2,0),那么d(P,A)=1;如果点集A所表示的图形是边长为2的正三角形及其内部,那么点集D={P|0<d(P,A)≤1}所表示的图形的面积为6+π.分析 如果集合A={(x,y)|x+y=1(0≤x≤1)},设Q(x,y),运用两点的距离公式,结合二次函数的最值,即可得到最小值;讨论P的位置,得到点集D={P|0<d(P,A)≤1}所表示的图形为三个边长分别为2,1的矩形和三个半径为1,圆心角为120度的扇形以及内部,运用面积公式计算即可得到.
解答 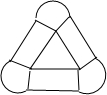 解:如果集合A={(x,y)|x+y=1(0≤x≤1)},设Q(x,y),
解:如果集合A={(x,y)|x+y=1(0≤x≤1)},设Q(x,y),
点P的坐标为(2,0),则|PQ|=$\sqrt{(x-2)^{2}+{y}^{2}}$=$\sqrt{(x-2)^{2}+(1-x)^{2}}$
=$\sqrt{2{x}^{2}-6x+5}$=$\sqrt{2(x-\frac{3}{2})^{2}+\frac{1}{2}}$,由于0≤x≤1,即有x=1取得最小值1,
那么d(P,A)=1;
如果点集A所表示的图形是边长为2的正三角形及其内部,
若P在正三角形及其内部,则面积为0,
若P∉A,则点集D={P|0<d(P,A)≤1}所表示的图形为
三个边长分别为2,1的矩形和三个半径为1,圆心角为120度的扇形以及内部,
即有面积为3×2×1+3×$\frac{1}{3}$π=6+π,
故答案为:1,6+π.
点评 本题考查新定义:点P到集合A的距离的理解和运用,考查集合的含义和运算能力,属于中档题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
12.设变量x,y满足约束条件$\left\{\begin{array}{l}{x-y-2≤0}\\{3x+y-6≥0}\\{y≤3}\end{array}\right.$,则z=-2x+y的最小值为( )
| A. | -7 | B. | -6 | C. | -1 | D. | 2 |
17.将函数$y=cos(\frac{1}{2}x-\frac{π}{6})$图象向左平移$\frac{π}{3}$个长度单位,再把所得图象上各点的横坐标缩短到原来的一半(纵坐标不变),所得图象的函数解析式是( )
| A. | $y=cos(x+\frac{π}{6})$ | B. | $y=cos\frac{1}{4}x$ | C. | y=cosx | D. | $y=cos(\frac{1}{4}x-\frac{π}{3})$ |
7.当n=5时,执行如图所示的程序框图,输出的S值是( )


| A. | 7 | B. | 10 | C. | 11 | D. | 16 |
11.已知集合A={x|y=$\sqrt{1-x}$},B={y|y=x2},则A∩B=( )
| A. | (-∞,1] | B. | [0,+∞) | C. | (0,1) | D. | [0,1] |
 已知函数$f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$的图象的一部分如图所示.
已知函数$f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$的图象的一部分如图所示.