题目内容
已知i是虚数单位，z=i+2i2+3i3+4i4，则|z|=
2
| 2 |
2
．| 2 |
分析：利用虚数单位i的幂运算性质化简复数z，再根据复数的模的定义和求法求得|z|．
解答：解：由于 z=i+2i2+3i3+4i4=i-2-3i+4=2-2i，故|z|=
=2
，
故答案为 2
．
| 4+4 |
| 2 |
故答案为 2
| 2 |
点评：本题主要考查虚数单位i的幂运算性质，复数的模的定义和求法，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
已知i是虚数单位，z=1-i，则
+z2对应的点所在的象限是（ ）
| 2 |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
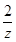＋z2对应的点所在的象限是