题目内容
已知f（x）=-x2+ax-b，a、b∈[0，4]，a、b∈R，则f（1）＞0的概率为______．
∵a、b∈[0，4]，
∴0≤a≤4，0≤b≤4，对应区域的面积为4×4=16，
由f（1）＞0得a-b-1＞0，
对应的平面区域为直线a-b-1=0的下方，
作出对应的平面区域如图：（阴影部分），
则当a=4时，b=3，即A（4，3），
当b=0时，a=1，即B（1，0），
则△ABC的面积S=
×3×3=
，
则由几何概型的概率公式可知f（1）＞0的概率为
=
，
故答案为：
．
∴0≤a≤4，0≤b≤4，对应区域的面积为4×4=16，
由f（1）＞0得a-b-1＞0，
对应的平面区域为直线a-b-1=0的下方，
作出对应的平面区域如图：（阴影部分），
则当a=4时，b=3，即A（4，3），
当b=0时，a=1，即B（1，0），
则△ABC的面积S=
| 1 |
| 2 |
| 9 |
| 2 |
则由几何概型的概率公式可知f（1）＞0的概率为
| ||
| 16 |
| 9 |
| 32 |
故答案为：
| 9 |
| 32 |
练习册系列答案
口算题天天练系列答案
相关题目
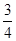，用满8000小时不坏的概率为
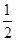.现有一只此种电子元件，已经用满3000小时不坏，还能用满8000小时的概率是________．