题目内容
 (2012•杭州二模)已知抛物线C:x2=2py(p>0),其焦点F到直线x-y-1=0的距离为
(2012•杭州二模)已知抛物线C:x2=2py(p>0),其焦点F到直线x-y-1=0的距离为| 5 |
| 8 |
| 2 |
(Ⅰ)求抛物线C的方程;
(Ⅱ)若△ABC的三个顶点在抛物线C上,顶点B 的横坐标为1,且直线BA,BC的倾斜角互为补角,过点A、C分别作抛物线C 的切线,两切线相交于点D,当△ADC面积等于4时,求直线BC的斜率.
分析:(Ⅰ)根据抛物线的焦点F到直线x-y-1=0的距离为
,可得
=
,从而可求抛物线C的方程;
(Ⅱ)可得B(1,1),设A(x1,x12),C(x2,x22),将直线AB、BC方程与抛物线方程联立,确定A、C的坐标,设出DC,AD的方程,联立解得D的坐标,表示出△ACD的面积,进而可确定直线BC的斜率.
| 5 |
| 8 |
| 2 |
|0-
| ||
|
| 5 |
| 8 |
| 2 |
(Ⅱ)可得B(1,1),设A(x1,x12),C(x2,x22),将直线AB、BC方程与抛物线方程联立,确定A、C的坐标,设出DC,AD的方程,联立解得D的坐标,表示出△ACD的面积,进而可确定直线BC的斜率.
解答:解: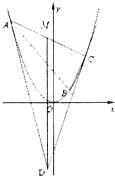 (Ⅰ)抛物线C:x2=2py(p>0)的焦点F(0,
(Ⅰ)抛物线C:x2=2py(p>0)的焦点F(0,
)
∵焦点F到直线x-y-1=0的距离为
∴
=
∴p=
∴抛物线C的方程为x2=y;
(Ⅱ)∵△ABC的三个顶点在抛物线C上,顶点B 的横坐标为1,
∴B(1,1)
设A(x1,x12),C(x2,x22),直线BC方程为y-1=k(x-1)
由
,消去y可得x2-kx+k-1=0
∴1+x2=k,∴x2=k-1,∴C(k-1,(k-1)2)
同理A(-k-1,(k+1)2),线段AC的中点M的坐标为(-1,k2+1)
y′=2x,则设DC:y-(k-1)2=2(k-1)(x-k+1);AD:y-(k+1)2=-2(k+1)(x+k+1)
联立解得D(-1,1-k2)
连接DM,则|DM|=2k2
∴△ACD的面积S=
×2k2(|k-2|+|k|)
当k≥2时,S=k2(2k-2)>8>4,所以k无解;
当0≤k<2时,S=2k2=4,解得k=
;
当k<0时,S=k2(2-2k)=4,解得k=-1,
综上所述,直线BC的斜率为
或-1
 (Ⅰ)抛物线C:x2=2py(p>0)的焦点F(0,
(Ⅰ)抛物线C:x2=2py(p>0)的焦点F(0,| p |
| 2 |
∵焦点F到直线x-y-1=0的距离为
| 5 |
| 8 |
| 2 |
∴
|0-
| ||
|
| 5 |
| 8 |
| 2 |
∴p=
| 1 |
| 2 |
∴抛物线C的方程为x2=y;
(Ⅱ)∵△ABC的三个顶点在抛物线C上,顶点B 的横坐标为1,
∴B(1,1)
设A(x1,x12),C(x2,x22),直线BC方程为y-1=k(x-1)
由
|
∴1+x2=k,∴x2=k-1,∴C(k-1,(k-1)2)
同理A(-k-1,(k+1)2),线段AC的中点M的坐标为(-1,k2+1)
y′=2x,则设DC:y-(k-1)2=2(k-1)(x-k+1);AD:y-(k+1)2=-2(k+1)(x+k+1)
联立解得D(-1,1-k2)
连接DM,则|DM|=2k2
∴△ACD的面积S=
| 1 |
| 2 |
当k≥2时,S=k2(2k-2)>8>4,所以k无解;
当0≤k<2时,S=2k2=4,解得k=
| 2 |
当k<0时,S=k2(2-2k)=4,解得k=-1,
综上所述,直线BC的斜率为
| 2 |
点评:本题考查抛物线的标准方程,考查抛物线的切线,考查三角形的面积的计算,解题的关键是利用点到直线的距离公式,确定切线方程,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012•杭州二模)已知正三棱柱ABC-A′B′C′的正视图和侧视图如图所示.设△ABC,△A′B′C′的中心分别是O,O′,现将此三棱柱绕直线OO′旋转,在旋转过程中对应的俯视图的面积为S,则S的最大值为
(2012•杭州二模)已知正三棱柱ABC-A′B′C′的正视图和侧视图如图所示.设△ABC,△A′B′C′的中心分别是O,O′,现将此三棱柱绕直线OO′旋转,在旋转过程中对应的俯视图的面积为S,则S的最大值为