题目内容
P是椭圆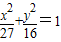
上的点，则P到直线l：4x+3y-25=0的距离的最小值为 ．
【答案】分析：由P是椭圆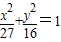
上的点，知P（3
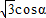，4sinα），从而得到P到直线l：4x+3y-25=0的距离d=
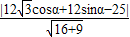，由此能求出P到直线l：4x+3y-25=0的距离的最小值．
解答：解：∵P是椭圆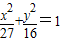
上的点，∴P（3
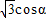，4sinα），
∴P到直线l：4x+3y-25=0的距离
d=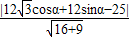
=
，
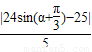∴当sin（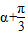
）=1时，
P到直线l：4x+3y-25=0的距离的最小值dmin=
．
故答案为：
．
点评：本题考查椭圆上的点到直线的距离的最小值的求法，解题时要认真审题，注意椭圆的参数方程和三角函数的恒等变换的合理运用．
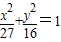上的点，知P（3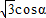，4sinα），从而得到P到直线l：4x+3y-25=0的距离d=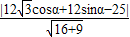，由此能求出P到直线l：4x+3y-25=0的距离的最小值．解答：解：∵P是椭圆
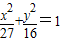上的点，∴P（3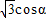，4sinα），∴P到直线l：4x+3y-25=0的距离
d=
=
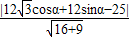
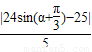，∴当sin（
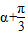）=1时，P到直线l：4x+3y-25=0的距离的最小值dmin=
．故答案为：
．点评：本题考查椭圆上的点到直线的距离的最小值的求法，解题时要认真审题，注意椭圆的参数方程和三角函数的恒等变换的合理运用．
练习册系列答案
名校课堂系列答案
相关题目
椭圆
+
=1的右焦点为F，设A（-
，
），P是椭圆上一动点，则|AP|+
|PF|取得最小值时点P的坐标为（ ）
| x2 |
| 5 |
| y2 |
| 4 |
| ||
| 2 |
| 3 |
| 5 |
| A、（5，0） | ||||||
| B、（0，2） | ||||||
C、（
| ||||||
| D、（0，-2）或（0，2） |
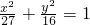上的点，则P到直线l：4x+3y-25=0的距离的最小值为________．
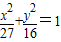上的点，则P到直线l：4x+3y-25=0的距离的最小值为 ．